Precalculus I Class 04/01

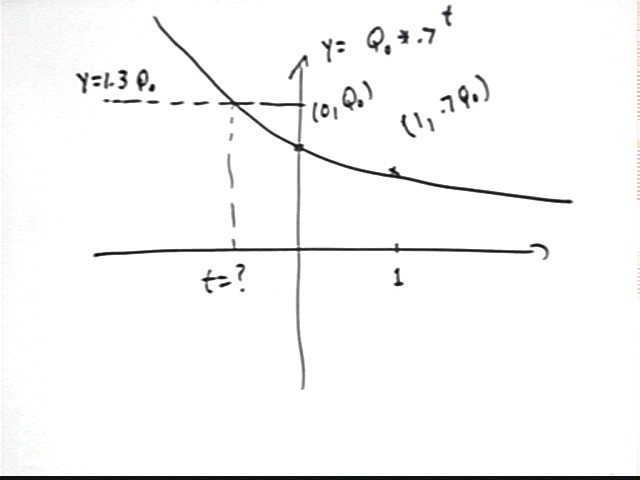
If Q(t) = Q0 * .7^t, then to two significant figures for what t is Q(t) equal to 1.3 Q0?

If Q(t) = 1.3 Q0 then Q0 * .7^t = 1.3 Q0.

So we need t such that Q0 * .7^t = 1.3 Q0.

We can simplify by multiplying both sides by 1/Q0 to get

.7^t = 1.3.

Pre-logarithms we can solve by trial and error. 

A basic-points graph of Q(t) has basic points (0, Q0) and (1, .7 Q0).  The x axis is a horizontal asymptote.  Our basic points show us that we have a decreasing exponential, so the asymptote is along the positive x axis.

y = 1.3 Q0 occurs for a horizontal line above Q0; we can estimate where this occurs.  We note that the corresponding t value is negative.

So we do trial and error with negative values of t.

The value is reasonably close to t = -1, which is a good starting point for a trial-and-error investigation.

We could also use logarithms.  We already have the equation .7^t = 1.3.  We easily solve using logarithms:

At what t does Q(t) = Q0 * .7 ^t reach .01 of its original value?

We first need to interpret the phrase '.01 of its original value'.   

So we need to solve the equation Q(t) = .01 Q0.  Since Q(t) = Q0 * .7^t, we have

Q0 * .7^t = .01 Q0.

Multiplying both sides by 1 / Q0 we get

.7^t = .01.

We can solve by trial and error or by logarithms.

I've written down two numbers.  When I multiply them together I get 0.  Tell me the value of at least one of my numbers.

One number gotta be 0.  The only thing we can multiply a nonzero number by to get 0 is 0.

For what value(s) of x does the function y = f(x) = (x-3)(x+4)(x-7)^2 equal zero?

The expression is a product of 4 factors, (x-3), (x+4), (x-7) and (x-7).  If the product is zero then at least one of the factors is zero.

So the zeros of this function occur at x = 3, -4, 7 and 7.

What do these results tell us about the graph of f(x) = (x-3)(x+4)(x-7)^2?

The graph passes through the points (-4,0), (3,0), (7,0) and (7,0).

What other graph point can we most  easily find?

It's easy to plug in x = 0, which will give us the y intercept.  We get y = (0-3)(0+4)(0-7)^2 = -3 * 4 * (-7)^2 = -588.

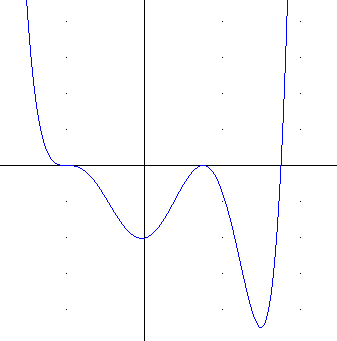
The figure below gives a sketch of what we know so far about the graph.

Using the five points (-4,0), (3,0) and (7,0), which are the only points at which the graph can pass thru or meet the x axis, and the point (0, -588), which is the only point at which the graph can pass thru the y axis, is it possible to construct a graph of the function?

We can make some guesses.  However, given any of the points at which the graph meets the x axis, we don't know whether the graph passes through that point going upward, going downward or whether it might even  just touch the axis, as does the vertex of a parabola. 

The figures below show a variety of graphs which pass through these points.  Note that the y scale of each graph is different, as you can tell by the location of the y-intercept, which in every case is (0, -588).

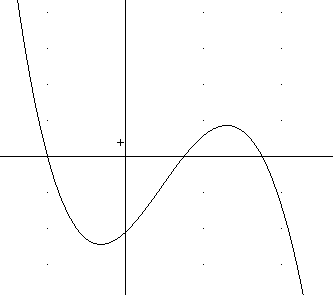
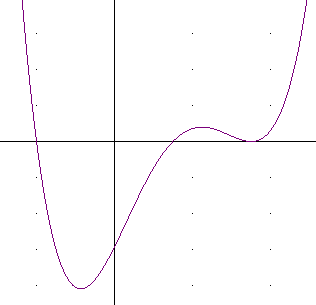
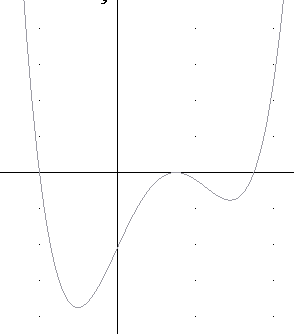
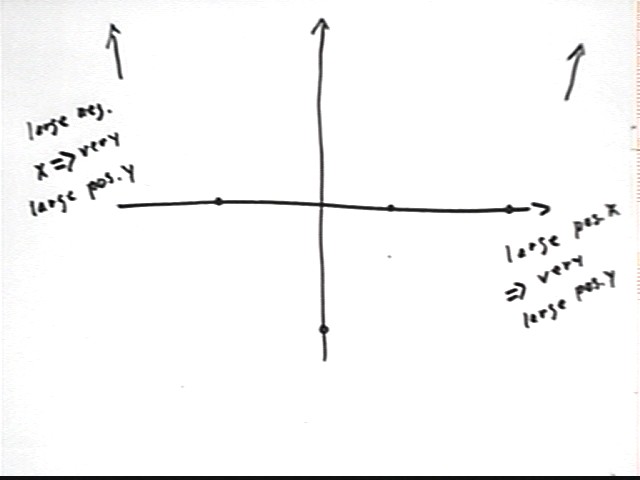
To get a better idea of how the graph behaves we can analyze the 'far-left' and 'far-right' behavior of this function.  If x is 'far to the left' then x is a large negative number--meaning a negative number with a large magnitude.  In this case the zeros lie between x = -4 and x = 7.  A 'large' value of x for polynomial function is one that lies quite a bit further from the origin than any of the zeros.  So a large negative x, for example, might be x = -100, or even x = -1000 or x = -1,000,000.  If x is a large negative number, is y = (x-3)(x+4)(x-7)^2 positive or negative, and would you describe this number as small, large, very large, or really, really, really large?

If x is a large negative number then every factor is a large negative number (i.e., (x-3), (x+4), (x-7) and (x-7) are all large negative numbers), so y is a product of four large negative numbers.  The product of four large negative numbers is positive, and the product of four large numbers is a very, very, very large number.    So when x is a large negative number, y is a very, very, very large positive number.

If x is a large positive number, is y = (x-3)(x+4)(x-7)^2 positive or negative, and would you describe this number as small, large, very large, or really, really, really large?

If x is a large positive number then every factor is a large positive number (i.e., (x-3), (x+4), (x-7) and (x-7) are all large positive numbers), so y is a product of four large positive numbers.  The product of four large positive numbers is positive, and the product of four large numbers is a very, very, very large number.  So when x is a large positive number, y is a very, very, very large positive number.

What do we now know about the graph?

We know that as we approach the first zero (-4, 0) from the left we are coming from very, very, very large y values.  So the graph must descend as we move from the left toward (-4, 0).

We know that as we leave the last zero, at (7, 0), we must begin approaching very, very, very large positive y values, so the graph must begin rising steeply.

See the figure below.

Can you sketch a graph with the given characteristics:  very, very, very large positive values at far left and far right, passing through the axes only at the four indicated points?

If we start at far left and descend to the first zero at (-4, 0), then pass through the y axis at the y intercept, then upward through the x axis at (3, 0) then back down through the x axis at (7, 0) we won't be able to get back up through the x axis to approach the large positive values at far right, as depicted below.

We could try something like the graph depicted below, where we pass through or meet the x axis in a variety of strange ways and do manage to achieve our far left and far right behavior.   The near-parabolic nature of the graph near x = 3 allows us to achieve the necessary zero at that point without actually going through the x axis, so we can end up approaching large positive values of y at both far left and far right.  However there is no particular reason why this should happen at x = 3 as opposed to x = -4 or x = 7.  And there is no apparent reason why we might want to 'flatten' the graph as it passes thru (-4, 0).

At which of the three zeros, x = -4, x = 3, or x = 7, would you expect the graph to act like a parabola?  What therefore does your graph look like?

Since the zero at x = 7 occurs as a result of the squared factor (x-7)^2, and (x-7)^2 indicates a basic y = x^2 parabola shifted 7 units to the right, the most reasonable expectation is that the parabolic behavior will occur at x = 7.

This will result in a graph much like the one depicted below.  An accurate graph generated by DERIVE is also depicted for comparison.

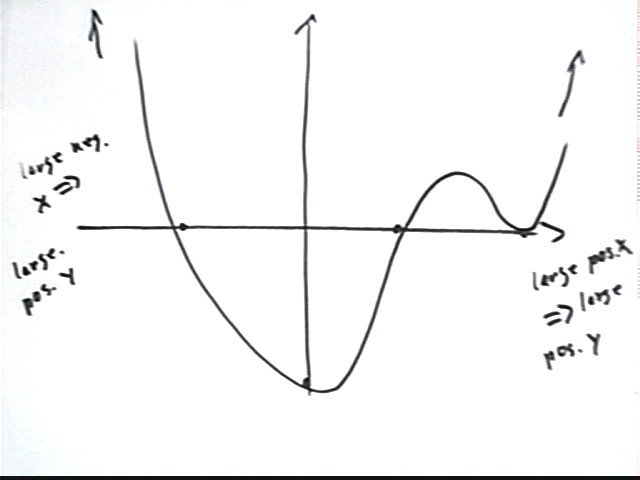
In what ways does the DERIVE graph differ from the sketched graph?

The low point of the sketched graph occurs to the right of the y axis, whereas the low point of the actual graph occurs well to the left of the y axis.  The relative peak between y = 3 and y = 7 is closer to y = 3 than to y = 7, contrary to the sketched graph.  And that peak is a bit lower on the DERIVE graph.