Precalculus I Class 04/08
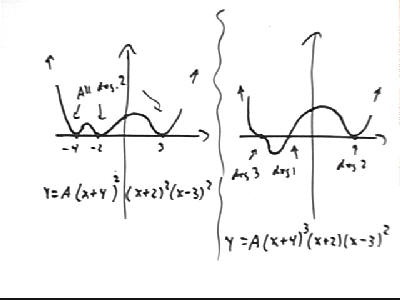
The graphs below both represent a polynomial of degree six with exactly three x value at which we get y = 0.
In the first all zeros are of degree 2, so the graph is very nearly parabolic near these points.
In the second one zero is of degree 3, resulting in a graph that levels off for an instant just as it passes thru the x axis. Another is of degree 1, passing through the x axis in a line which near the zero is very nearly straight, and the other is degree 2, giving us a near-parabola near the zero.

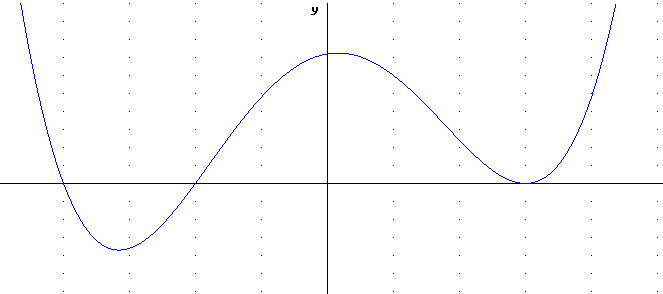
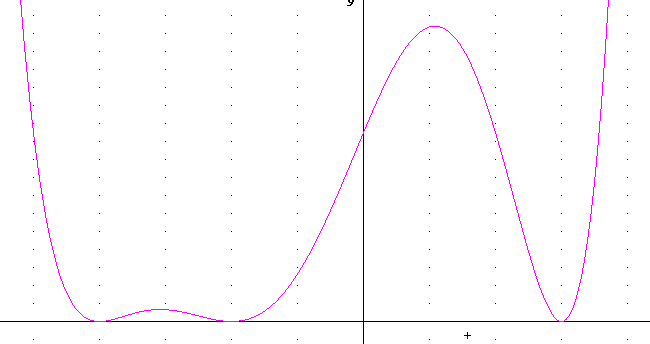
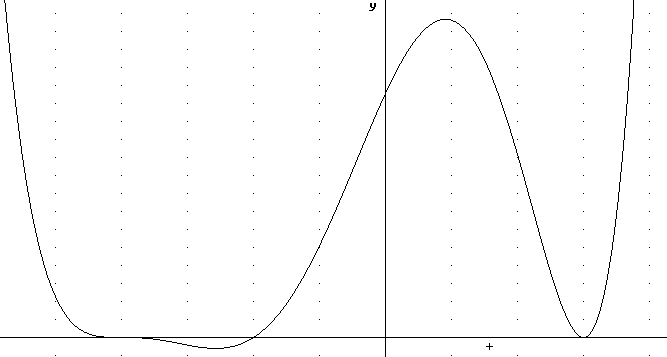
The three graphs below all have exactly three x-intercepts, as in the examples above.
All three also appear to be of even degree, since for large positive as well as large negative x they appear to approach +infinity.
In the graph immediately below the zeros appear to have degrees 1, 1 and 2, indicating a total degree of at least 4.
The next graph appears to have three zeros of degree 2, giving it total degree at least 6.
This graph appears to have zeros of degree at least 3, 1 and 2, for total degree at least 6.
The graph below could represent y = A(x+4)(x+2)(x-3)^2, with its first-degree zeros at x = -4 and x = -2 and its second-degree zero at x = 3.
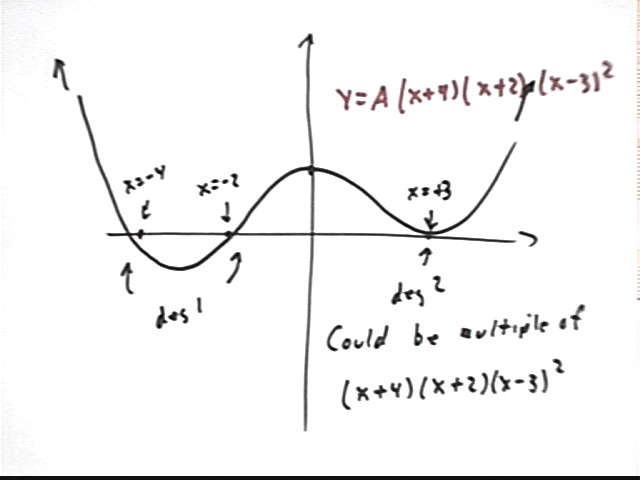
A more accurate graph of this function:

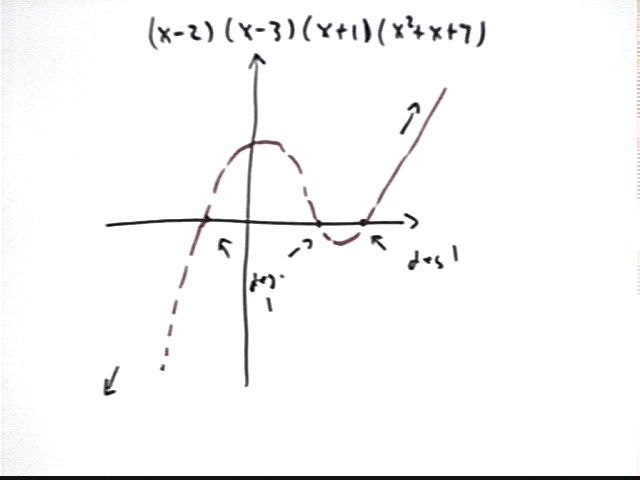
It could also conceivably represent y = A(x+4)(x+2)(x-3)^2 * (x^2 + x + 7), because (x^2+x+7) is an arbitrary irreducible quadratic (one we just picked out of a hat containing all irreducible quadratics).
x^2 + x + 7 is an irreducible quadratic because it has no zeros.
If we set x^2 + x + 7 = 0 and try to solve using the quadratic formula our solution will include sqrt(b^2 - 4 a c) = sqrt(1^2 - 4 * 1 * 7) = sqrt(-27), showing that there are no real values of x for which the expression is zero.
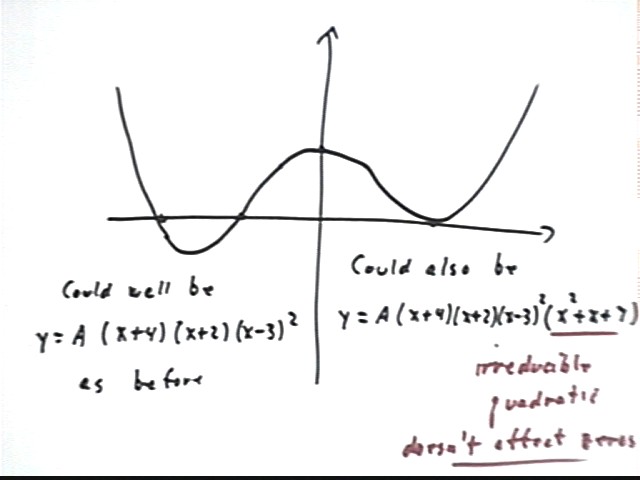
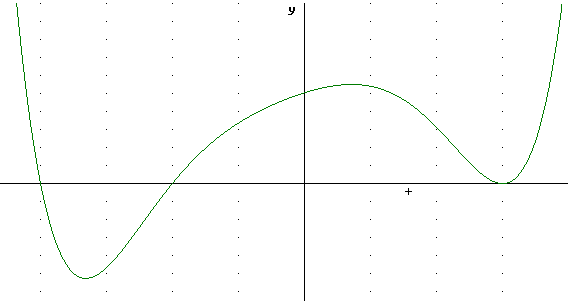
The irreducible quadratic x^2 + x + 7 has vertex at x = -b / (2a) = -1/2. The vertex is its 'low point' so it tends to 'depress' values more near x = -1/2 than away from that point. This causes a little less symmetry in the curve, as opposed to the preceding graph. Note how the curve between x = -2 and x = 3 appears to be a bit more lopsided than in the preceding graph.
Suppose we know that a polynomial has degree 5. What is the maximum number of zeros it could have?
An example of a polynomial of degree 5 might be (x-3)(x-2)(x-1)(x+1)(x+2). This polynomial has 5 zeros, all different. We say that the polynomial has 5 distinct zeros.
If everyone in the class made up their own degree-5 polynomial with no zeros in common with the given polynomial it's very likely that they would all be different.
Suppose we know that a polynomial has degree 5. In how many different ways can we have, say, exactly 3 different numbers that give us zeros?
One possibility would be something like (x-2)^2 (x-1) (x+1)^2, with two of the zeros having degree 2. This polynomial actually has five zeros, since it can be written (x-2)(x-2)(x-1)(x+1)(x+1), but the zeros x = 2 and x = -1 are repeated zeros, each being repeated twice. Thus there are only three different numbers that give us zero, even though there are five zeros.
Another possibility might be of the form (x-2)^3 (x-1)(x+1), with one zero of degree 3 and the other two of degree 1.
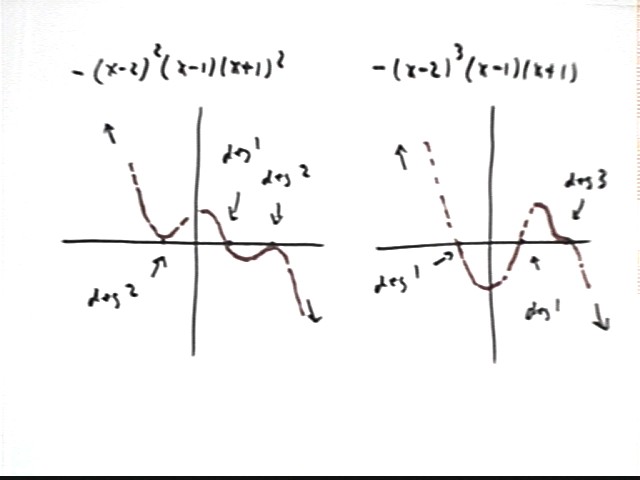
There is one more way we can get a degree-5 polynomial with exactly three different numbers that give us zero. That is to use an irreducible quadratic, as in the example (x-2)(x-3)(x+1)(x^2 + x + 7).
If the zeros are at -2, -1 and 1 then the following are examples of different ways to get polynomials of degree five with exactly three different x values for which the polynomial is zero:
(x-2)^2 (x-1) (x+1)^2
(x-2)^3 (x-1)(x+1)
(x-2)(x-3)(x+1)(x^2 + x + 7)
How can we have a degree 5 polynomial with exactly 4 numbers that give us zero? Sketch such a graph.
We can repeat one of the five zeros, for example getting (x-3)(x-2)^2(x-1)(x+1).