Precalculus I Class 04/10

Note:  Due to ongoing problems accessing the web server it is not clear how long it will take to get these pages completed.

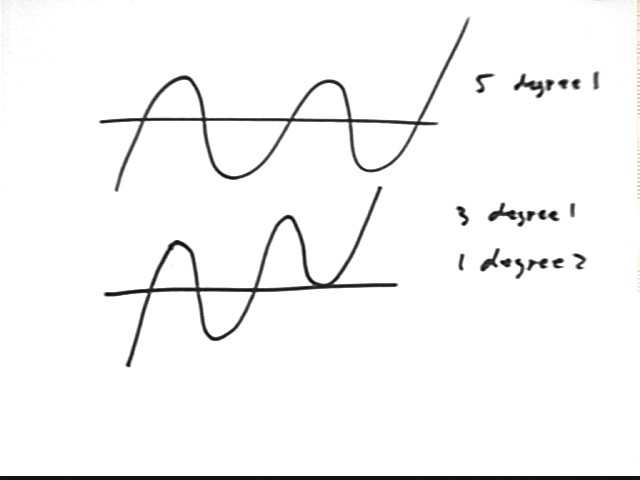
For a degree-5 polynomial we can have any of the following:

• 5 first-degree zeros (e.g., (x-3)(x-2)(x+4)(7x-9)(2x+1) )
• 1 second-degree zero and 3 first-degree zeros ( (x-2)^2 (x+3)(x-7)(2x+4) )

• 2 second-degree zeros and 1 first-degree zero (e.g., (x-5)^2 (x-2)^2 (x-1) )
• 1 third-degree zero and 2 first-degree zeros (e.g., (x+5)^3(x-3)(x+2))

• 1 third-degree zero and 1 second-degree zero (e.g., (x-2)^3 (x+3)^2)
• 1 fourth-degree zero and 1 first-degree zero (e.g., (x+5)^4 (x-2) )

• 1 fifth-degree zero  (e.g., (x-5)^5 ).

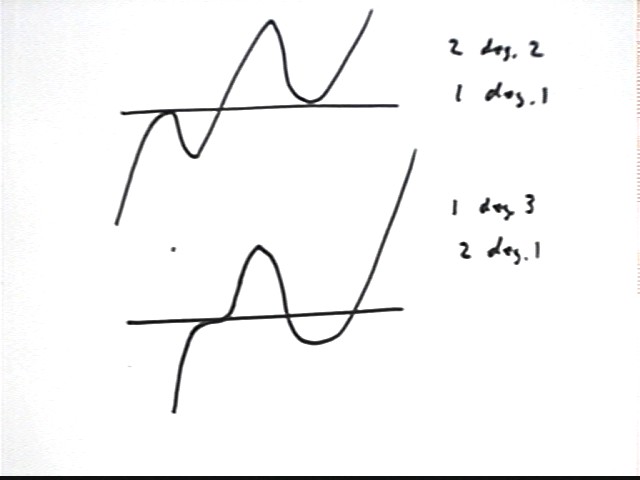
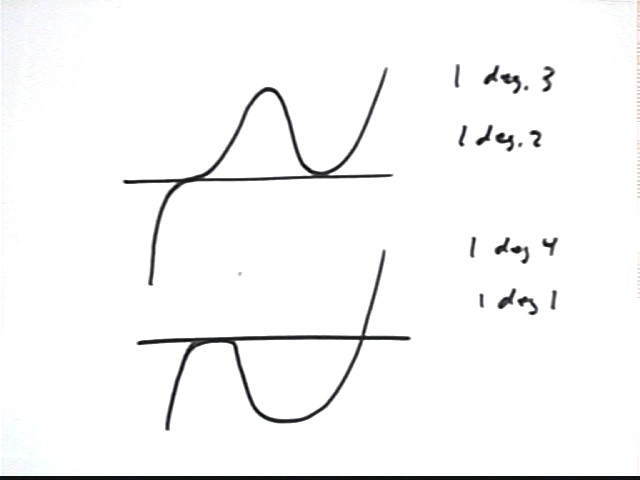
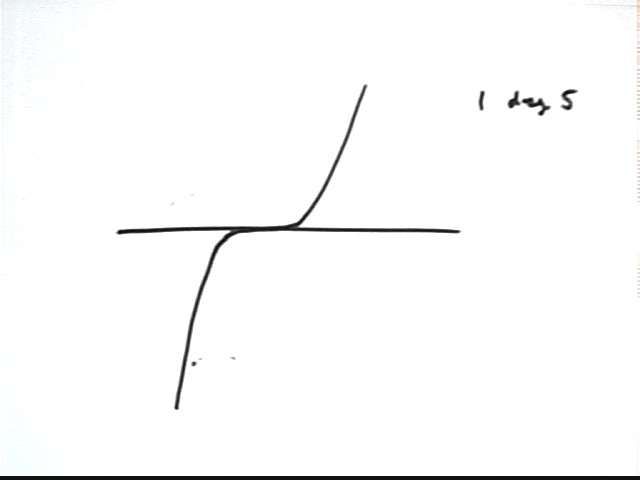
We aren't done yet.  We do have a list of every possible combination of five linear factors.  However we haven't yet considered what happens if we have an irreducible quadratic (or two).

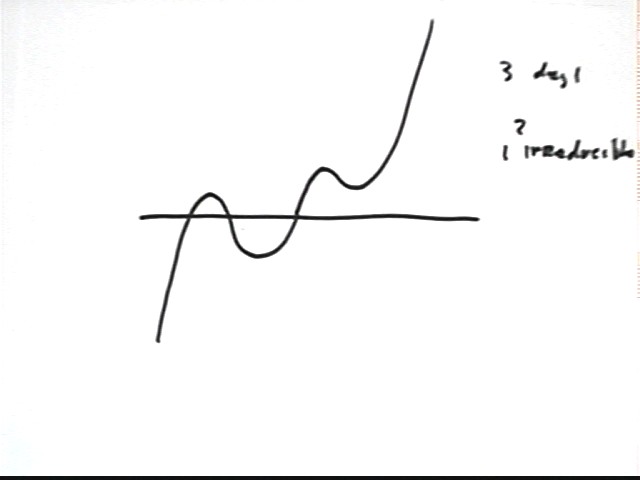
If there is one irreducible quadratic then we can have

• 3 first-degrees zeros and our irreducible quadratic (e.g., (x-3)(x+4)(x-7)(x^2 + x + 7))

• 1 second-degree zero, 1 first-degree zeros and our irreducible quadratic (e.g., (x-3)^2(x-7)(x^2 + x + 7))

• 1 third degree zero and our irreducible quadratic (e.g., (x-3)^3 (x^2 + x + 7))

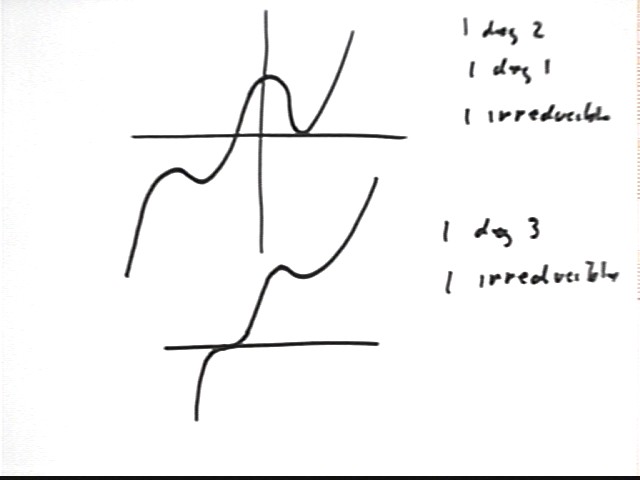
We can also have two irreducible quadratics.  If so we must have one first-degree zero:

• 2 irreducible quadratics make up degree 4; to get degree 5 we need one more linear factor.  (e.g., (x-3)(x^2+x+7)(x^2+10)

Evaluate e^x at x = .01, .1 and .2. 

Evaluate 1 + x at x = .01, .1 and .2.

Evaluate 1 + x + x^2 / 2 at x = .01, .1 and .2.

e^.01 = 1.01005

1+.01 = 1.01.  Note that this 'misses' e^.01 by .00005.

1+.01+.01^2 = 1.01010.  This 'misses' e^.01 by .00005.

e^.1 = 1.10517

1+.1 = 1.1 'misses' e^.1 by about .005

1+.1+.1^2/2 = 1.105 'misses' e^.1 by about .00017

e^.2 =1.22140

1 + .2 = 1.2 'misses' e^.2 by about .021

1 + .2 + .2^2/ 2  = 1.22 'misses' e^.2 by about .001