0429

Precalculus I Class 04/29

We start with 1 pair of matched baby rabbits.

It takes a month for a pair of baby rabbits to become sexually mature.

A pair of rabbits which are sexually mature at the beginning of one month will produce a matched pair of sexually mature baby rabbits at the beginning of the next month, and for every month thereafter.

Rabbits never die.

How many pair will there be at the end of each of the first 10 months?

Month	# baby pairs	# mature pairs	total # pairs
0	1	0	1
1	0	1	1
2	1	1	2
3	1	2	3
4	2	3	5
5	3	5	8
6	5	8	13
7	8	13	21
8	13	21	34
9	21	34	55
. . .	. . .	. . .	. . .
n-2			a(n-2)
n-1		a(n-2)	a(n-1)
n	a(n-2)	a(n-1)	a(n)

Our conclusion is that the rule for the sequence is

a(n) = a(n-1) + a(n-2), with
a(0) = a(1) = 1.

The meaning is that

a(n-2) rabbits were alive two months ago and were hence mature one month ago, contributing a(n-2) pairs of baby rabbits in the present month
a(n-1) rabbits were alive one month ago and will hence be alive and mature in the present month.

A more extensive table is shown below:

month	immature	mature	total	ratio of seq
0	1	1	1
1	1	1	1	1
2	1	1	2	2
3	1	2	3	1.5
4	2	3	5	1.67
5	3	5	8	1.6
6	5	8	13	1.625
7	8	13	21	1.615384615
8	13	21	34	1.619047619
9	21	34	55	1.617647059
10	34	55	89	1.618181818
11	55	89	144	1.617977528
12	89	144	233	1.618055556
13	144	233	377	1.618025751
14	233	377	610	1.618037135
15	377	610	987	1.618032787
16	610	987	1597	1.618034448
17	987	1597	2584	1.618033813
18	1597	2584	4181	1.618034056
19	2584	4181	6765	1.618033963
20	4181	6765	10946	1.618033999
21	6765	10946	17711	1.618033985
22	10946	17711	28657	1.61803399
23	17711	28657	46368	1.618033988
24	28657	46368	75025	1.618033989
25	46368	75025	121393	1.618033989
26	75025	121393	196418	1.618033989
27	121393	196418	317811	1.618033989
28	196418	317811	514229	1.618033989
29	317811	514229	832040	1.618033989
30	514229	832040	1346269	1.618033989
31	832040	1346269	2178309	1.618033989
32	1346269	2178309	3524578	1.618033989
33	2178309	3524578	5702887	1.618033989
34	3524578	5702887	9227465	1.618033989
35	5702887	9227465	14930352	1.618033989
36	9227465	14930352	24157817	1.618033989
37	14930352	24157817	39088169	1.618033989
38	24157817	39088169	63245986	1.618033989
39	39088169	63245986	102334155	1.618033989
40	63245986	102334155	165580141	1.618033989
41	102334155	165580141	267914296	1.618033989
42	165580141	267914296	433494437	1.618033989
43	267914296	433494437	701408733	1.618033989
44	433494437	701408733	1134903170	1.618033989
45	701408733	1134903170	1836311903	1.618033989
46	1134903170	1836311903	2971215073	1.618033989
47	1836311903	2971215073	4807526976	1.618033989

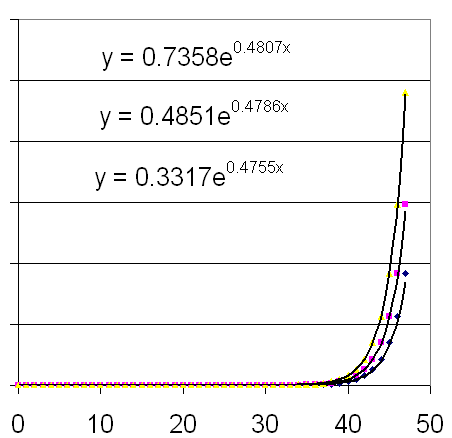
The ratios of the sequence are found by dividing each total by the preceding total. The sequence of totals is 1, 1, 2, 3, 5, 8, 13, ... and the ratios are 1/1 = 1, 2/1 = 2; 3/2 = 1.5; 5/3 = 1.6, etc..

We note that the ratios appear to approach a limit which to 10 significant figures is 1.618033989. Recalling that a constant ratio is a characteristic of an exponential function we hypothesize that this sequence can be approximated by an exponential function and move to Excel to fit an exponential curve to our results.

Excel in fact gives us three data sequences, one corresonding to the number of immature rabbits, a second to the number of mature rabbits and a third to the sequence of totals. These three curves are shown below along with the exponential functions that approximate them, with the horizontal axis representing the month and the vertical the number of rabbits.

The lowest of the curves corresponds to the numbers of immature rabbits, the highest to the total number of rabbits. The three curves all have the same form, y = A e^(kx), with k taking approximately the same value for all three (k values range from .4755 to .4807). The values of A range from .3317 to .7358.

We note that since the total is equal to the number of mature rabbits plus the number of immature rabbits, the top curve represents the approximate sum of the two lower curves. You should see how for any x value the y values on the top curve respresent the sum of the y values of the two lower curves.

Note also that the sum of the two lower functions is pretty close to the upper function. If A and k are represented to 2 significant figures the functions are y = .33 e^(.48 x), y = .48 e^(.48 x) and y = .74 e^(.48 x). These again correspond to the number of immature rabbits, the number of mature rabbits and the total number of rabbits. This is pretty nearly true, with .33 e^(.48 x) + .49 e^(.48 x) = .72 e^(.48 x), close to the approximation .74 e^(.48 x).

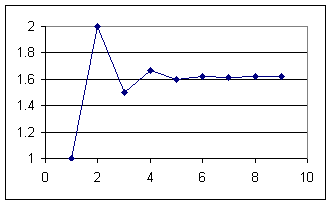
The sequence of ratios is plotted below with a vertical scale from 1 to 2. We see how the sequence increases then decrease alternately, with any two consecutive y values 'squeezing' all the subsequent y values between them (e.g., the first two y values are 1 and 2, and all subsequent y values are between 1 and 2; the next two are 2 and 1.5, and all remaining y values are between 2 and 1.5; etc. ).

From this picture we see that the sequence appears to converge to a value a little greater than 1.6.

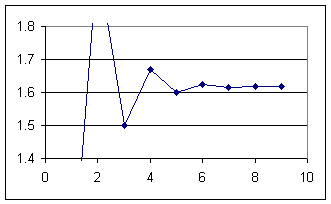
Plotting the sequence of ratios again, with y values ranging only from 1.4 to 1.8, exaggerates the vertical scale. From this graph we can estimate that the sequence converges to a value around 1.62.

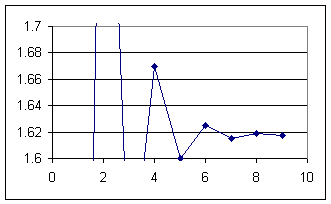
We again plot the sequence with a reduced vertical scale, again showing how the alternately increasing and decreasing behavior of the sequence continues.

This graph shows that the sequence converges to a value slightly less than 1.62.

The convergent value of the sequence is in fact (1+sqrt(5))/2. This is an irrational number, with an infinite number of significant figures. To 10 significant figures this value is 1.618033989; note that the ratios take this 10-significant-figure value starting with the 24th month.

Suppose I take a 1000 mg dose of super-duper-make-ya-better medicine. I take a dose every 6 hours.

In 6 hours I lose 60% of whatever medicine I had in my system just after the previous dose.

So how much do I have just after I take my second dose?

How much do I havc after each of the first 5 doses?

The 1000 mg present just after the first dose decreases by 60%, leaving 40% of the 1000 mg still present. 40% of 1000 mg is 400 mg, so just before the second dose we have 400 mg. Just after the second 1000 mg dose we therefore have 1400 mg.

The 1400 mg present just after the second dose decreases by 60%, leaving 40% of the 1400 mg still present. 40% of 1400 mg is 560 mg, so just before the third dose we have 560 mg. Just after the third 1000 mg dose we therefore have 1560 mg.

The 1560 mg present just after the third dose decreases by 60%, leaving 40% of the 1560 mg still present. 40% of 1560 mg is 624 mg, so just before the fourth dose we have 624 mg. Just after the fourth 1000 mg dose we therefore have 1624 mg.

The same process leads us to the conclusion that just after the fifth dose we have 1649.6 mg.

dose #	amt after dose	amt just before next dose
1	1000	400
2	1400	560
3	1560	624
4	1624	649.6
5	1649.6	658.6

The sequence of amounts in mg is 1000, 1400, 1560, 1624, 1649.6. Is this sequence exponential?

The ratios of the sequence are 1400/1000 = 1.4, 1560 / 1400 = 1.11, 1624/1560 = 1.04, etc.. These ratios are not constant so we cannot conclude from the ratios of the sequence that the sequence is exponential.

A sequence is also exponential if the ratio of its differences is constant. The differences of the sequence are 400, 160, 64 and 25.6. The ratios of these differences are all .4, so the sequence is indeed exponential.

dose #	amt after dose	differences
1	1000
2	1400	400
3	1560	160
4	1624	64
5	1649.6	25.6

The convergent value of this sequence is the concentration for which the 60% lost is equal to the 1000 mg taken with each dose. We therefore find the value C such that 60% of C is 1000 mg.

Solving the equation .60 C = 1000 we obtain C = 1000 / .60 = 1666 2/3.

From the figure below we see that the concentrations 1000, 1400, 1520, ... will exponentially approach the asymptote C = 1666 2/3.

If we find the deviations between these concentrations and the asymptotic value C = 1666 2/3 we obtain for doses 1, 2, 3, 4 and 5 the deviations 666 2/3, 266 2/3, 106 2/3, 42 2/3 and 17 1/16.

These deviations are modeled by the exponential function

deviation = 666 2/3 * e^(-.9163(t-1) ) = 666 2/3 * .4^(t-1).

Since the function that models drug concentration is [ concentration = 1666 2/3 - deviation ] we conclude that the concentration is modeled by the function

C(t) = 1666 2/3 - 666 2/3 e^(-.9163(t-1) ) = 1666 2/3 - 666 2/3 * .4^(t-1).