based on data by Physics 121 student lp
From T = period vs. L = length data for a pendulum we obtain a table of T vs. L.
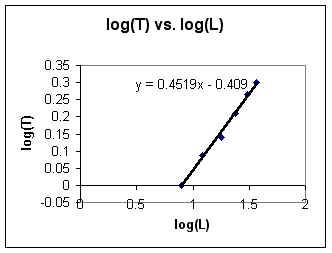
We create a table of log(T) vs. log(L) and graph this table.
We draw a straight line fitting the points. The line indicated below is the best-fit regression line.
The slope of the line is p = .45 and the y intercept (found by extending the line until it hits the y axis) is y0 = -.41.
The equation of T vs. L is T = 10 y0 * L p.
It follows that T = 10-.41 * L.45 = .39 L.45
Details of the analysis are shown below the figure. You should understand these details.

At L = 12, 18, 24 inches you got T = 1.22, 1.38 and 1.62 seconds.
These values are to be compared with the predicted periods.
The predicted periods, based on T = .39 L^.45, would be 1.19, 1.43, 1.63, comparing favorably to your values .9, 1.22, 1.38 and 1.62.
The error with the first point is 1.22 - 1.19, which is .03.
This is about 3% of the observed .9.
The residuals (differences between data values and predictions) are .3, -.5 and -.1.
The corresponding errors are between .1% and .4%, which is very good accuracy.
We have y = .45 x - .41, approximately.
Thus log(T) = .45 log(L) - .41.
So 10log(T) = 10.45 log(L) - .41 = 10-.41 * 10.45 log(L) = .39 * [ 10log(L) ] .45 = .39 * L.45.
10log(T) = T, so we have T = .39 L.45.
Theoretically, from physics, we should have T = 2 `pi ( L / g ) .5.
For g = 9.8, we have T = .4 L.5.
This compares favorably with T = .39 L.45.