class 050709

Each of the graphs below depicts three points on the graph of a quadratic function of the form y = a x^2.  Every graph has vertex (0, 0). 

• Quickly sketch the parabola corresponding to each graph.
• Sketch the x and y axes for each graph.  The locations of the x and y axes will follow the graphs around; they won't be in the same position for every graph.
• The specific functions for the three of these graphs are y = 1/2 x^2, y = -x^2 and y = 2 x^2.  Label each of these graphs with its function.
• What is the function for the remaining graph?  Label that graph with its function.
• Suppose that instead of going through the vertex, the x axis runs along the bottom of each graph and the y axis along the left edge.  What then would be the coordinates of the vertex of each graph? 

graph 1

graph 2

graph 3

graph 4

Tables for y = 1/2 x^2, y = -x^2 and y = 2 x^2 are as follows:

In Graph 1 the points one unit to the right and left of the vertex are displaced -1 units in the y direction from the vertex, matching the behavior of the function y = - x^2.

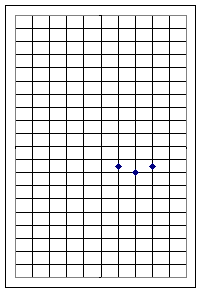
In Graph 2 the points one unit to the right and left of the vertex are displaced +2 units in the y direction from the vertex, matching the behavior of the function y =  2 x^2.

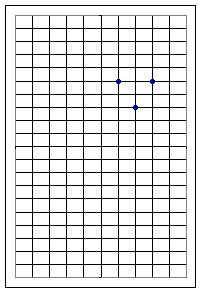
In Graph 3 the points one unit to the right and left of the vertex are displaced +1/2 units in the y direction from the vertex, matching the behavior of the function y = 1/2 x^2.

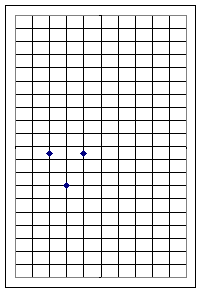
In Graph 4 the points one unit to the right and left of the vertex are displaced +2.5 units in the y direction from the vertex, matching the behavior of the function y = 2.5 x^2.

If the x and y axes correspond respectively to the bottom and left edges of the grid then:

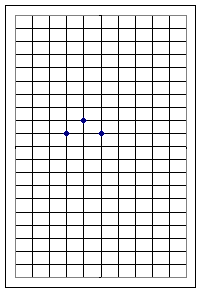
For graph 1, the vertex lies at (4, 12).

For graph 2, the vertex lies at (7, 13).

For graph 3, the vertex lies at (7, 8).

For graph 4, the vertex lies at (4, 7).

How would the graph of y = - x^2 have to be shifted to give us a similar parabola whose vertex is (4, 12)?

The vertex of the y = - x^2 parabola is (0, 0), so the y = -x^2 parabola would have to be shifted 4 units to the right and 12 units up.

The shift to the right could be accomplished by replacing x with x - 4 to get the function y = - (x - 4) ^ 2.  It's easy to see that if x = 4, this function gives us y = 0, and that x = 3, x = 4 and x = 5 give us y values -1, 0 and -1, as shown in the table below:

This shifts our 3 basic points to x coordinates x = 3, x = 4 and x = 5.

If we now add 12 to our y values we obtain y = - ( x - 4 ) ^ 2 + 12, which matches our graph:

What are the vertex and the graph points 1 unit to the right and left of the axis of symmetry for the function y = 2 x^2 - 8 x + 3?  Sketch these three points on the fourth of the above graphs, and based on these points sketch the corresponding parabola.

Questions and Answers:

To find the zeros of a quadratic function do you simply substitute 0 in for the y and then solve for the x?

Right.

Substitute 0 for y, which will give you a quadratic equation of the form 0 = a x^2 + b x + c. Then solve using the quadratic formula.

I am still unsure about the x vs. y concept. Is there a definitive way to know for sure which information should be classified as x or y. Thanks.

y vs. x means y on the vertical and x on the horizontal axis. x vs. y would put x on the vertical and y on the horizontal, which is not the traditional way of graphing functions. The quantity before the 'vs.' is on the vertical.

Generally y will stand for the independent variable and x for the dependent variable. It's usually but not always easy to tell which is independent and which dependent. For example depth depends on the clock time; the clock keeps going independent of what happens in the cylinder. The period of a pendulum depends on its length, not vice versa.

I know how ""aX^2"" widens or narrows the parabola in a graph, but how does ""bX"" and ""c"" move the vertex on the graph.

It's not easy to understand from the y = a x^2 + b x + c form just how b works with a to determine the axis of symmetry, then how these quantities work with c to determine the y coordinate of the vertex. The rules are simple enough:

the axis of symmetry occurs at x = - b / (2 a) and the y coordinate of the vertex is obtained by substituting this x into the function.

Why they work is the harder question.

To understand the answer to this question we have to consider the other form of the quadratic, which is

y = a ( x - h)^2 + k.

a is the same for both forms. h and k are the x and y coordinates of the vertex. We will spend a good bit of time in class discussing how h and k affect the graph. In a nutshell:

if x in the function y = a x^2 is replaced by x - h then in any y vs. x table the y values will 'shift down', which corresponds to shifting the graph to the right, by h units and

the y values will all be increased by k.

When finding the zeros of the vertex do you substitue zero for y or x or both in the quadratic equation? Will it work if the graph doesnt touch the zero on either axis?

The zeros are the points where the graph meets the x axis, and they correspond to y = 0.

If the graph doesn't touch the x axis then there are no real zeros. This is the case if the quadratic formula ends up with a negative under the square root sign. Since the square root of a negative number is not a real number, the quadratic formula would in this case tell you that there are no real zeros.

Some of the data sets contain numbers with several decimal places which can become very confusing in an equation, is it possible to round the numbers in the original data set without severely changing the final outcome of the modeling process?

Yes. The deviation from the ideal quadratic behavior is typically at least a few units, and when this is the case it wouldn't hurt a thing to round off to two or three significant figures.

My question is, on the precal homework you assigned on wed., I'm having some trouble finding the vertex, like on finding the vertex and graphing y=x^2+x+1 I used the formula (-b)/(2a) to find the vertex coordinate x. my a = 1 b=1 c=1 then my first thing would to be divide -(1)/(2(1)) This would be -(1/2) which would equal my x coordinate then I substitute the x coordinate into y=x^2+x+1 for x and find y to be (7/4)

Then I am confused on how to find my unit to the left and my unit to the right, I was just wondering whether I did this right, I read over the worksheets, but I'm still confused. Thanks

You correctly found the vertex to be (-1/2, 7/4).

The axis of symmetry is the vertical line x = -1/2.

One unit to the right of the axis of symmetry we have x = +1/2. Substitute this into the equation and you will get the y coordinate 1 unit to the right.

One unit to the left of the axis of symmetry we have x = +1/2. Substitute this into the equation and you will get the y coordinate 1 unit to the left.

Your results will agree with the rule that the points 1 unit to the right and 1 unit to the left are a units from the vertex. For this function a = 1, and these points both lie 1 unit higher than the vertex.

I have a question about problem 2 on exercise 1-3(Graphs of Quadratic Functions) it is the last part of the question where it says ...Sketch the graph of each function, based only on the 3 points you have sketched and your knowledge that the graph is a parabola... I dont understand what to do because the question up from that one kinda answers that question also. What do I do differently in that question than I did in the previous question?

One question asks you to graph the three points. The other asks you to sketch the curve based on those three points.

I also have a question about #4 on that same worksheet...If you were to draw a smooth curve passing through the vertex of each of the first four graphs, what can you say about the shape of the curve?...What do you want to know about them? The only thing that I can see is that they are all four turning upward....is that all I need to say?

Your statement that 'they are all four turning upward' is a little ambiguous. It states that every point is turning upward, and a point can't turn upward. You might either mean that the trend of the curve through the vertices is turning upward, or you might mean that every graph is turning upward.

Don't give it away, but I'll tell you that the curve through those vertices is itself a parabola. We'll look at it more closely in class.

One of the instructions was to graph 3 points: the vertex, one point to the right and one to the left of the vertex. To graph the 2 points to the right and left of the vertex, all you do is move one to either the left or right and then up whatever spaces that ""a"" equals to right?

Exactly. Good question, which you answered yourself.