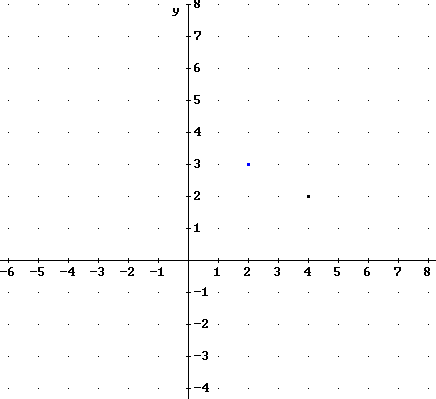class 050923
Note the Access link 23-24-242 containing all questions asked
to date, with answers.
No calculators are to be used on these questions:
Make a table for the function y = 2^x for x values -3, -2, -1,
0, 1, 2, 3, and sketch a graph of this function (2 minute time limit).
Two points are marked on the graph below.
Please answer the following assuming that the two points lie
on the graph of a function y = f(x):
- What would be the coordinates of these points if the
graph of f(x) was vertically stretched by factor 2?
- What would be the coordinates of these points if the
graph of f(x) was vertically shifted -5 units?
- What would be the coordinates of these points if the
graph of f(x) was horizontally shifted 3 units?
- What would be the coordinates of these points if the
graph of f(x) was first vertically stretched by factor 2, then vertically
shifted -5 units?
- What would be the coordinates of these points if the
graph of f(x) was first vertically shifted -5 units, then vertically
stretched by factor 2?
- What would the coordinates of the corresponding points be
on the graph of y = 3 f(x)?
- What would the coordinates of the corresponding points be
on the graph of y = f(x + 3)?
- What would the coordinates of the corresponding points be
on the graph of y = f(x) + 3?
- What would the coordinates of the corresponding points be
on the graph of y = 2 f(x+3) - 5?
- If y represents depth in cm and x represents clock time
in seconds, then what is the average rate of change of depth with respect to
clock time between the points?
- If f(x) = x^2, then what is the expression for 2 f(x+3) -
5? What points on the graph of the second function correspond to the
three basic points of the first?
- If f(x) = 2^x, then what is the expression for 2 f(x+3) -
5? What points on the graph of the second function correspond to the
two basic points of the first? What will be the asymptote for the
second function?
Problem: Sketch a graph of the basic exponential function y = 2^x. Give the algebraic form of the function obtained if this function is stretched vertically by factor -2.62 then shifted .34 units vertically. Sketch a graph of this new function, and show that the graph is different than that obtained if the vertical shift precedes the vertical stretch.
This is very confusing.
How do you plug in both the horizonal and vertical stretch into the equation?
Compared to y = f(x), y = A f(x - h) + c is vertically stretched be factor A, horizontally shifted h units and vertically shifted c units.
The given vertical stretch factor is A = -2.62, there is no horizontal shift so the horizontal shift is h = 0, and the vertical shift is c = .34.
So for the given stretches and shifts the function would be -2.62 f( x - 0 ) + .34, which for the function f(x) = 2^x would be
-2.62 * 2^(x - 0) + .34, or just
-2.62 * 2^x + .34.
Concerning the test in general, is there a specific website we have to go to to obtain the actual test, or will www.vhcc.edu/pc1fall9 be enough?
From that page you just click on the Tests 'button' across the top of the page, and follow instructions as given in class (see the notes from class on 050921).
Here is a copy of those instructions:
Go to the Learning Lab.
Go to your homepage at http://vhmthphy.vhcc.edu/ and click on Tests.
Print off the test.
Get it signed by the attendant.
Take it in the room to which the attendant directs you.
Hand it to the attendant.
I am working on another question from the major quiz which asks: Find the zeros of the quadratic function y=.024t^2+-2t+63, yet when I use the quadratic formula to find the zeros, I get an imaginary number by means of the square root of b^2-4ac. This surely can't be right. Please help me find my error.
This can certainly happen. If you get a negative under the square root, you don't have a solution.
The statement of the quadratic formula says that 'if y = a t^2 + b t + c , then y = 0 if and only if t = ( - b +- sqrt(b^2 - 4 a c ) ) / (2a)'.
If there is a negative under the square root, t is not a real number and there are therefore no real-number zeros.
This implies that the graph lies either entirely above or entirely below the t axis.
If you check out the vertex and the points 1 unit right and 1 unit left of the vertex, you will find that the vertex lies above the t axis and the other two points lie .024 units higher than the vertex, showing that the parabola opens upward. If a parabola opens upward and its vertex is above the axis, then the whole parabola is above the axis and never crosses it, so there are no real zeros.
The number under the square root is called the discriminant. If the discriminant is negative, therefore, there are no real zeros.
If the discriminant is zero, the you have +- 0 in the numerator, so both the + and the - solution will be identical.
If the discriminant is positive, then you have a real square root and the + and - give you two different real numbers. So a positive discriminant implies two real zeros.