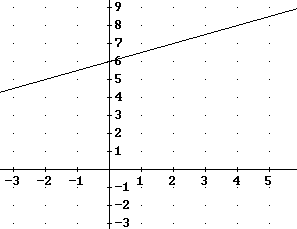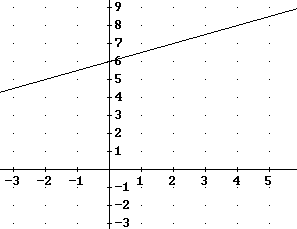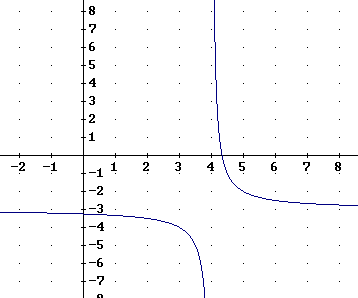class 051007
What are the basic points of the basic linear, quadratic and
power functions?
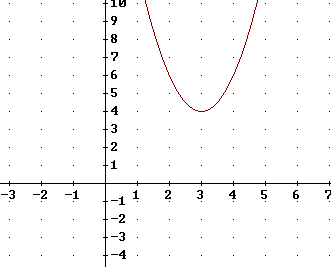
The first graph below represents a linear function, the second
represents a quadratic function and the third represent a p = -1 power function.
- Mark the basic points on each of these graphs.
- How would the basic function for each graph be stretched
and/or shifted to get the graph of the function shown?
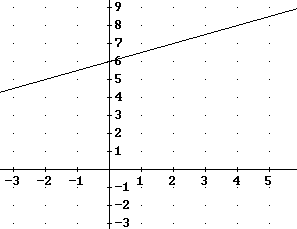
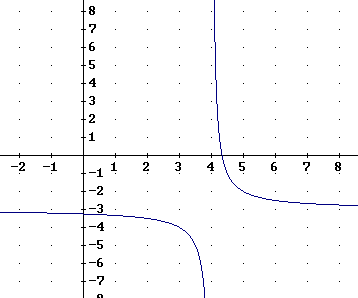
What are the basic points for y=f(x)?
The answer depends on the function f(x).
The basic linear function is y = x and its basic points are
the x = 0 and x = 1 points.
The basic quadratic function is y = x^2 and its basic points
are the x = -1, x = 0 and x = 1 points.
The basic points of the exponential function y = 2^x are the
x = 0 and x = 1 points, and also the horizontal asymptote at the negative x
axis. The asymptote isn't really a point but we include it among the three basic
things we need in order to quickly graph an exponential function.
The basic points of a power function y = x^p are the x = -1,
x = 0, x = 1/2, x = 1 and x = 2 points. If p is negative, then the x = 0 'point'
isn't really a point but a vertical asymptote, and as the trend of basic points
shows, for negative p the x axis is a horizontal asymptote in both directions.
If a function is of the form y = A f(x-h) + k then the basic
points (and all points) are 'stretched' to positions A times as far from the x
axis, horizontally shifted h units and vertically shifted k units. By applying
this principle just to the basic points, we can quickly and easily locate the
graph of A f(x-h) + k for any of our basic functions.
The basic points of y = A f(x-h) + k are the points you get
when you apply these stretches and shifts to the basic points of the function
f(x).
Difference Equations
f(0) = 2
f(1) = 5
f(2) = 8
f(3) = 11
etc.
The pattern here goes up by 3 and starts at 2. In more
precise language we say
f(0) = 2
f(n+1) = f(n) + 3.
To use this, we first let n = 0.
Substituting 0 for n into f(n+1) = f(n) + 3 we get
f(0+1) = f(0) + 3
f(1) = 2 + 3
f(1) = 5.
Next, we let n = 1. Substituting 1 for n into f(n+1) =
f(n) + 3 we get
f(1 + 1) = f(1) + 3
f(2) = f(1) + 3. Since f(1) = 5 from the previous step:
f(2) = 5 + 3
f(2) = 8.
Next, we let n = 2. Substituting 2 for n into f(n+1) =
f(n) + 3 we get
f(2 + 1) = f(2) + 3
f(3) = f(2) + 3. Since f(2) = 8 from the previous step:
f(3) = 11.
It's clear that this process just keeps adding 3 to the
previous value to get the next value.
What linear function f(x) would give us the same values?
A graph of f(n) vs. n goes up 3 for every unit of run so its
slope is 3.
The graph goes through (0, 2) so the y intercept is 2.
The function is therefore y = m x + b with m = 3 and b = 2.
The function is y = 3x + 2.
The linear function y = f(x) = m x + b can be modeled by the
equations
f(0) = b
f(n+1) = f(n) + m.