class 051010

These questions are from your homework on the worksheet entitled 'The Slope = Slope Equation". Using the homework you have done, quickly give answers to these questions:

1. If we know that (3, -4) is a data point on a line with slope 2.8, what is the equation of the line?

2. Find the linear function depth(t) = mt + b if it is known that at clock time 30 seconds the depth is 50 centimeters, and that depth is changing at a rate of -.35 centimeters/second.

5. Suppose a line passes through (3, -2) with slope 5. What is the slope = slope equation (y - y1) / (x - x1) = m when we substitute these values? What do we get when we solve for y?

Substitute the above values x = 3, y = -2 and m = 5 into the form y = mx + b. Solve for b. Then substitute m and b into the form y = mx + b to obtain the equation of the line.

Compare the equations you obtained from the different methods.

Make a statement about whether or not the two methods seem to give the same results.

8. Assume that the average class grade in this course is a linear function of how many hours of intelligent out-of-class effort students put into it, on the average. Suppose that an average of 40 hours of such effort was sufficient to make an average grade, on a 4-point scale, of 1.2, and that each additional hour added .045 points to this average. Find the linear function pointAverage(aveHours) that models this situation.

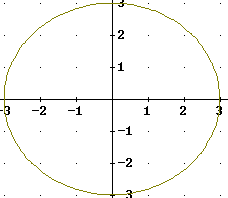
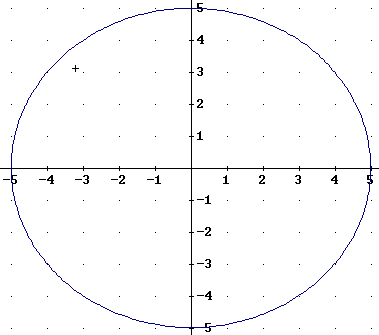
The two figures below contain circles of radii 3 and 5, respectively. Answer the following:

How many grid dots are in the smaller circle?
How many grid dots are in the larger circle?
What is the ratio of the number of grid dots in the larger circle to the number in the smaller?
What is the ratio of the radius of the larger circle to that of the smaller?

Most people count 29 dots on in the smaller circle and 77 dots in the larger.

We note that the area of the smaller circle is pi r^2 = pi ( 3^2) = 9 pi = 28.3, approx., while the area of the larger is pi (5^2) = 78.5 approx..

The number of dots is pretty close to the area.

The unit of area is a square 1 unit on a side.

Does the larger square have more or less than double the diameter of the smaller?

The diameter of the smaller circle is 6 and the diameter of the larger is 10. Double the diameter of the smaller is 12. So the second circle has less than double the diameter of the first.
Another way to look at this is that the diameter ratio of the second circle to the first is 10 / 6 = 1.67, approx.
Note that the diameter ratio is the same as the ratio of the radii, which is 5 / 3 = 1.67.
We also note that the ratio of circumferences is 1.67 ( 2 pi * 5 / ( 2 pi * 3) = 5 / 3 = 1.67).
In symbols it's easy to see that D2 / D1 = 2 r2 / (2 r1) = (2 / 2) * (r2 / r1) = r2 / r1, and similarly that c2 / c1 = (2 pi r2) / (2 pi r1) = r2 / r1.

Does the larger square have more or less than double the area of the smaller?

Based on the evidence of your counts, the larger has more than double the area of the smaller because 77 is more than double 29.
The ratio of areas is 77/29 = 2.7 approx..

How in the world could it have come to this? We've got a larger circle with less than twice the radius of the smaller, but it's got more than twice the area.

The area ratio is (A2 / A1) = ( pi r2^2) / ( pi r1^2) = pi / pi * r2^1 / r1^2 = r2^2 / r1^2 = (r2 / r1)^2.