You can substitute x values to make a table of this function. For example substituting x = -2, -1, 0, 1, 2 we get the table
| -2 | -0.75 |
| -1 | -1.5 |
| 0 | -3 |
| 1 | -6 |
| 2 | -12 |
and the graph
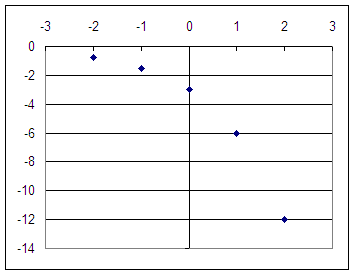
You would of course sketch a smooth curve for this function.
questions 050914
I don't really have anything that I need help with right at this moment. I
think that everything is going ok for now, but if I have any questions I will
know how to send them to you.
Part of the reason for the assignment is to engage skills related to the
process of thinking of and phrasing a good question. Everyone needs to do this.
My question is how can I sketch a graph for something like number 4
...Sketch the graph if the exponential
family y=A*2^x for the values A=-3 to 3.
I know that I can plug in -3 to 3 for A but what do I do for my x?
You will get a different function for each value of A.
If you plug in A = -3 then you get the function y = -3 * 2^x. For this
function
You can substitute x values to make a table of this function. For example substituting x = -2, -1, 0, 1, 2 we get the table
-2 -0.75 -1 -1.5 0 -3 1 -6 2 -12 and the graph
You would of course sketch a smooth curve for this function.
We would then plug in A = -2 and get a new table and graph.
The graph would be as indicated below:
After sketching the smooth curve, we see that this graph has a shape similar to the A = -3 graph, but that all the points are closer to the x axis.
We would continue in this manner, obtaining a series of 7 graphs for A values from -3 through 3.
All the resulting curves would be plotted on the same set of coordinate axes in order to show the family.
In the question, ""Where illunintation(distance)=50/distance^2,"" how
would you solve for illumination
(distance)/illumination(2*distance)?
<h3>You need to say what you do and do not understand about this situation.
There are two expressions in the expression illumination
(distance)/illumination(2*distance).
One is
illumintation(distance)
and the other is
illumination (2 * distance).
You are given that
illumination (distance) = 50 / distance^2.
From this it follows that
illumination (2 * distance) = 50 / (2 * distance)^2.
So
illumination (distance)/illumination(2*distance) = ( 50 / distance^2 ) / (50 /
(2 * distance)^2 ).
(a / b) / ( c / d) = (a / b) * ( d / c), so
( 50 / distance^2 ) / (50 / (2 * distance)^2 ) = ( 50 / distance^2 ) * (2 *
distance)^2 / 50.
50 / 50 = 1 so the expression is
(2 * distance)^2 / distance^2, which is equal to
2^2 * distance^2 / distance^2. Since distance^2 / distance^2 = 1, the final
result is just
2^2, or 4.</h3>
I don't really have anything that I need help with right at this moment. I think
that everything is going ok for now, but if
I have any questions I will know how to send them to you.
<h3>Part of the reason for the assignment is to engage skills related to the
process of thinking of and phrasing a good
question. Everyone needs to do this.</h3>
My question is about #10 on the introdution to function families...The
illumination y form a certian florescent bulb is given as a function of distance
x by the generalized power functionfor p=-1 with A=370, h=0 and c=0. Determine
the illumination at distance of 1, 2, 3, 4 units, and sketch a graph....
I'm not sure how to sketch the graph useing units 1 ,2 ,3
and 4...
Do I need to plug 1-4 into x?
The graph is rather hard to sketch because the numbers are so large...
Thanks.
<h3>The generalized power function is y = A ( x - h)^p + k, so the function
for p=-1 with A=370, h=0 and c=0 is
y = 370 ( x - 0) ^ -1 + 0, or just
y = 370 x^-1.
So you just plug in x = 1, 2, 3 and 4, make a table of y vs. x and plot the
graph.
If the numbers are large then you label your graph accordingly.</h3>
The following is the only problem that gave me trouble on the homework. The
(t+3) and (t+3)/(t) really made me think and I'm
assuming that the way I have them is as simplified as they can get. Am I right?
Where value(t) = $1000 (1.07)^t
value(0)= 1000(1.07)^0 =1
value(1)= 1000(1.07)^1= 1070
value(2)= 1000(1.07)^2=1,144,900
<h3>Looks like you squared the 1000 as well as the 1.07. Just square the
1.07.</h3>
value(t+3)= 1000(1.07)^(t+3)=1070^(t+3)
<h3>You don't multiply 1000 by 1.07. The exponentiation precedes the
multiplication. So you just leave this as 1000(1.07)^
(t+3).</h3>
value(t+3)/value(t)= 1000(1.07)^((t+3)/(t))= 1070^((t+3)/(t))
<h3>value( (t+3) / t) = 1000(1.07)^((t+3)/(t)), but
value(t+3) / value(t) = 1000(1.07)^(t+3)/(1000 * 1.07^t).
This can be simplified.
Recall that a^(b + c) = a^b * a^c. So
$1000 ( 1.07)^(t + 3) =
$1000 ( 1.07)^t * (1.07)^3.
So
1000(1.07)^(t+3)/(1000 * 1.07^t) =
$1000 ( 1.07)^t * (1.07)^3 / ( $1000 * 1.07^t) =
1.07^3.</h3>
It says: sketch a resonable graph of y=f(x), if it is known that
f(2)=80, f(5)=40 and f(10)=25. I understand that, what I don't understand is how
to find the value of f(7) or when it says
to find the difference in x values between the points where f(x)=70 and where
f(x)=30?
<h3>Once you've sketched your graph you can estimate those values directly from
the graph. To get f(7) you start on the horizontal axis at 7, and go straight up
until you hit the graph, then over to the vertical axis. The value you hit on
the vertical axis is your estimate of f(7).
To find where f(x) = 70 you start at 70 on the vertical axis, go straight over
to the graph, then down to the x axis.
To find where f(x) = 30 you start at 30 on the vertical axis, go straight over
to the graph, then down to the x axis.
The distance between the points you meet on the x axis is the requested
difference in x values.</h3>
y=temperature=T(t), then what is the symbloic expression for each of the following: The temp. at the t=3....
I dont know where to start or what to do...
I read the generalized modeling process and I am clueless on what to do. I dont know if I need to pluge into the y=temp.=T(t) or what. I
do know that the little t's are given but thats about all I know.
<h3>You know that y = T(t).
You don't know the formula for T(t), so the best you can do for t = 3 is
substitute 3 for t to get T(3).
If t = (a + b) then T(t) becomes T(a + b).
Whatever t is, that's what you plug in for t.</h3>
The instructions say to find expressions of the given functions, are you supposed to solve them and if so how do you go about doing that?
<h3>I assume this is exercise #1 on the worksheet for f(x) notation. You need
to be specific when asking questions.
The instruction should read
'Of course you know, or at least suspect, that your function models won't always
be quadratic. Obtain the indicated expressions for the following functions, none
of which are quadratic:'
For example if the function was f(t) = t^5 and you were asked to find f(2),
f(3z) and f(a+b) your answers would be 2^5, (3z)^5 and (a + b)^5.</h3>
What is the equation for the vertex?
<h3>See also answers to previous questions and examples, especially the quiz
questions for 9/12/05.
The vertex of the parabola defined by y = f(t) = a t^2 + b t + c has t
coordinate
t_vertex = - b / (2 a).
The y coordinate is found by substituting this t coordinate into the function.
In function notation the vertex is located at the point
( -b/(2a), f(-b/(2a) ) ).</h3>
the directions are to write as full (decimal) numbers with standard units. #12b is 85""mu""V. I have never encountered V as a standard unit, I worked the problem as follows (85""mu""V)(1V/10^-6 ""mu""V)=85,000,000 V. Is this the correct?
This is very nearly correct. However mu V does not mean V / mu, it means mu *
V. Multiplication is understood if there is no symbol between the units.
So mu V means 10^-6 * V and the result would be
85 * 10^-6 * V = .000086 V.</h3>
I understand that when you try to find the vertex of a parabola you start
with X=-b/2a. Then do you just plug what you get for x back into the orginal
equation or do you do something else to find Y.
<h3>Just plug it back into the original equation. That gives you the y
coordinate of the vertex.</h3>