questions for 050912

I have no idea what do to on Exercises 3-4 ....Sketch a reasonable graph of y=f(x) if it is known that f(2)=80, f(5)=40 and f(10)=25.....

I dont know what kind of formula I need to use...I read all of the Introduction to the Generalized Modeling Process and found the formulas y=f(x)=ax^2+bx+c.

y=f(x)=Ab^x+c....
y=f(x)=mx+b...Do I use one of those? I am so lost!

You're not lost. You just need a little clarification on the instruction 'sketch a reasonable graph... '.

The instruction says to sketch a reasonable graph. You don't need to find a formula for the function.

If f(2) = 80 then the point (2, 80) will lie on the graph.
If f(5) = 40 then the point (5, 40) will lie on the graph.
If f(10) = 25 then the point (10, 25) will lie on the graph.

Sketch a graph containing these points. Then connect them with any reasonable smooth curve, and answer the questions based on your picture.

Of course you could substitute these coordinates for x and y in the model y = a x^2 + b x + c, as we did last week, and get the formula for a parabola through these three points. Then you could find the vertex and the points 1 unit right and left, and sketch a graph based on that model. However I say this just to remind you of that process, not because I want you to go to all that trouble here.

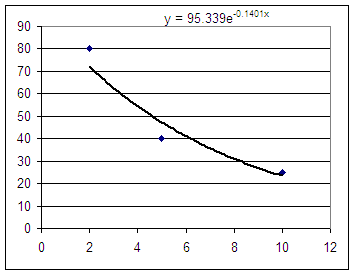
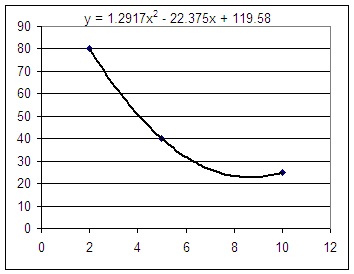
I couldn't put this into my posted reply, but here's a copy of the best-fit quadratic function:

Here's a copy of the best-fit power function:

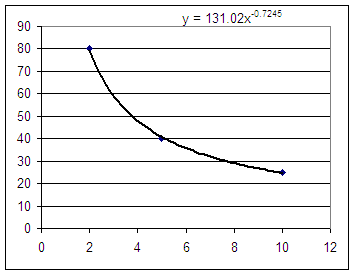
And here's a copy of the best-fit exponential function, which isn't worth much because Excel isn't smart enough to figure out the best asymptote.

You can see from at least the first two graphs that there's a lot of latitude in the graphs you could sketch to fit the function, so there's a lot of latitude in possible answers to the questions asked on the homework.

When there is a function notation problem that is, for instance, f(x)=2^x and you have to find for f(x+3), I know that the (x+3) replaces the x in 2^x, but then do you distribute the x and the 3 or do you just leave it as 2^(x+3)?

Good question. The expression you get is 2^(x+3) and that expression answers the question.

If you're going to simplify the expression, which isn't necessary on this question but is on some subsequent questions, you have to use the standard rules of algebra. In this case you need to use the laws of exponents.

Recall that a^(b + c) = a^b * a^c. So

2^(x+3) =
2^x * 2^3 =
2^3 * 2^x =
8 * 2^x.

Where value(t)=$1000(1.07)^t. When the value is (t+3) how do you find the answer for the unknown when you put the unknown back into the equation? Or is (t+3) in the equation the answer?

value(t+3)=$1000(1.07)^(t+3).

This could be simplified using order of operations and laws of exponents, but the for this question the answer is correct as shown above.

For future reference:

Recall that a^(b + c) = a^b * a^c. So

$1000 ( 1.07)^(t + 3) =
$1000 ( 1.07)^t * (1.07)^3.

We can calculate 1.07^3. We get something like 1.23. Your calculator will tell you whether my mental calculation was right, but if it was we then see that

$1000 ( 1.07)^t * (1.07)^3 =
$1000 ( 1.07)^t * 1.23 =
$1230 (1.07 ^ t),

approximately.

I would like to know how to solve the last problem on page 4 of 11 in the f(x) Notation: The Generalized Modeling Process packet.

I'm sorry because I'd like to answer. But while I have the document I don't have a copy of the packet, so I don't know what printed on what page.

Part of asking a question is to include a statement about what you do and do not understand about the situation, which would allow me to figure out what your question is.

Thanks for submitting the question, and I'll try to answer in class tomorrow once I've been able to locate the problem.