Solving a System of Quadratic Equations
Copy this document into your word processor, fill in the blanks and submit using the instructions at the end. To fill in a blank just place your cursor at the beginning, in the middle of or at the end of the blank, whichever you find more convenient, and type in your information.
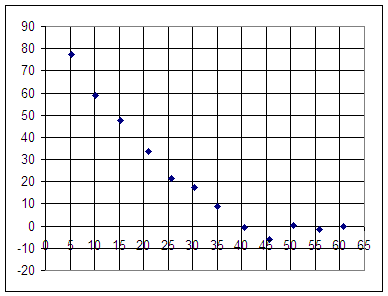
Assume the data set
| t | y |
| 5.972361 | 71.215 |
| 10.79718 | 59.98121 |
| 15.96633 | 42.06543 |
| 20.63604 | 33.06885 |
| 25.81026 | 20.23678 |
| 30.09933 | 14.67699 |
| 35.65546 | 7.958709 |
| 40.13297 | 1.515133 |
| 45.47234 | -2.41142 |
| 50.95876 | 1.146707 |
| 55.63397 | -1.54308 |
| 60.17647 | -0.30166 |
A graph of this data set follows:

Assume the model y = a t^2 + b t + c.
Fill in the blanks then copy and submit as instructed at the end.
1. Obtain 3 points on which to base your model and use those points to obtain three simultaneous equations for the parameters a, b and c:
Sketch the parabolic curve you think best fits the data.
Mark 3 points on your curve which do not coincide with data points.
Estimate as nearly as you can the coordinates of your three points.
Fill in the coordinates of your three points:
( , )
( , )
( , )
Based on your three points, the three equations we get by assuming the form y = a t^2 + b t + c are:
= a + b + c
= a + b + c
= a + b + c
2. Eliminate c from two of the equations:
When you subtract the first equation from the second what equation do you get?
a + b =
3. Eliminate c from a different set of two equations:
When you subtract the first equation from the third what equation do you get?
a + b =
4. Write down the resulting two equations in two unknowns:
What system of equations do you therefore solve to find a and b?
a + b =
a + b =
5. Eliminate b from these two equations:
To eliminate b we multiply the first equation by and the second by before adding the equations
The two equations we add are therefore
a + b =
a + b =
and the resulting equation is
6. Solve the resulting equation for a, then use back-substitution to find b:
Solving the equation, we obtain a = ?
Substituting this value back into the first of our two equations for a and b we get
* + b =
which after the multiplication gives us
+ b = .
Solving for b we obtain
b =
7. Back-substitute once more to find c:
Substituting into the first of our 3 equations for a, b and c we get
= * + * + * c , which after multiplication gives us
= + + * c . Solving for c we get
c = .
Our model is therefore
y = t^2 + t + .
8. When you solved for c you used the first equation, which came from your first data point. Now check your model by substituting the coordinates of your other points:
Substituting the coordinates of the third point into our model we get
= * + * + , which simplifies to
=
If we were to substitute the coordinates of the first point into our model what would we get?
=
If we were to substitute the coordinates of the second point into our model what would we get?
=
9. Use your model to answer questions about the situation:
According to this model, what equation do we get if we ask the question 'what is the value of y when t = 28'?
What do we get when we simplify or solve this equation? Include the details below:
According to this model, what equation do we get if we ask the question 'what is the value of t when y = 28'?
What do we get when we simplify or solve this equation? Include the details below:
10. Compare your results to the best-fit model:
Your results will not match the best-fit quadratic model for the entire data set. This is because of your rounding all values to the nearest .1, and also becaue the best-fit model takes account of all the data points, not just the three you chose.
The ideal best-fit model is y = 0.0359 t^2 - 3.6983 t + 93.229.
The graph of the data set and the best-fit quadratic is shown below:
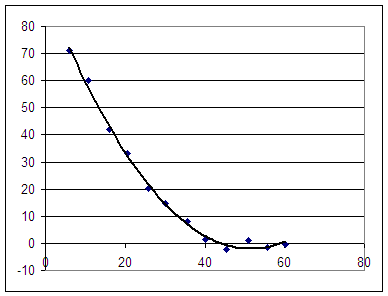
You chose three data points
According to the best-fit model:
For the t value of the first point you marked, the value of y would be , which differs from your estimated y value by .
For the t value of the second point you marked, the value of y would be , which differs from your estimated y value by .
For the t value of the third point you marked, the value of y would be , which differs from your estimated y value by .
Once you have completed this exercise, submit it as follows:
Open the form http://www.vhcc.edu/dsmith/class_work_form.htm .
Fill in your name, access code and course as requested on the form.
For the assignment code copy the following line into the box
quadSystem
Finally copy this entire document and paste it into Item 1, scroll to the bottom of the form and click Submit Form.