0830 Quiz

1.  Make a table for each of the following functions, using x values -3, -2, -1, 0, 1, 2 and 3:

• y = x^2
• y = sqrt(x)
• y = 2^x
• y = x
• y = 1 / sqrt(x)

Match each of the following graphs with one of the functions

• y = x
• y = x^2
• y = sqrt(x)
• y = 2^x
• y = 1 / sqrt(x)

and identify each as a linear, quadratic, exponential or power function.  Some functions might be in more than one of these classes; if so identify all classes to which the function belongs.

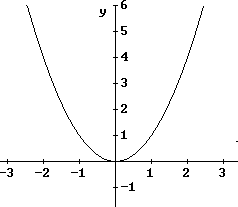
The above graph corresponds to y = x^2, which is a quadratic function and also a p = 2 power function (it is of the form y = a x^p for a=1 and p = 2).

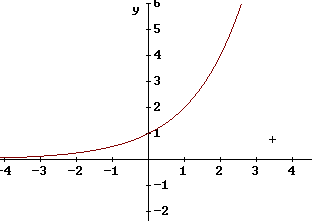
This is the graph of y = 2^x, which is the basic exponential function.  This is not a power function, since in a power function x is raised to the power p and in the present function x is the exponent, not the base.

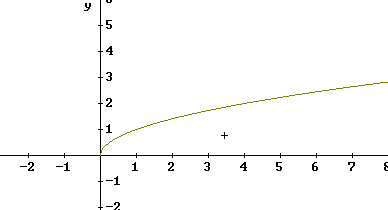
This is the graph of y = sqrt(x), which is undefined for x < 0 and which increases at a decreasing rate.

Since y = sqrt(x) is the same as y = x^(1/2), this is a power function.  Its form is y = a x^p for a = 1 and p = 1/2.

This is the graph of y = 1 / sqrt(x).  Since sqrt(x) increases with increasing x, the function 1 / sqrt(x) must decrease with increasing x (the bigger the number the smaller the reciprocal).

1 / sqrt(x) can be written as 1 / (x^(1/2)), which can also be written as x^(-1/2).

y = x^(-1/2) is a power function of form y = a x^p with a = 1 and p = -1/2.

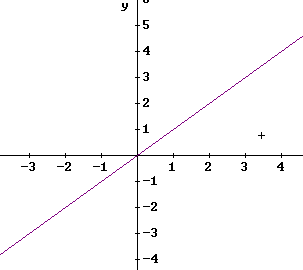
This is y = x, which is the basic linear function.

2.  Sketch a graph of each of the following sets of points and tell which of the functions in #1 you think the general shape of the graph is more similar to:

• The points (6, 100), (10, 10) and (20, 2).

This graph appears to have a vertical asymptote at the y axis and a horizontal asymptote at the x axis, as does the graph of y = 1 / sqrt(x).

• The points (5, 100), (10, 40) and (20, 150).

This graph starts high, comes to a low point then goes high again, like the basic quadratic function y = x^2.

• The points (2, 8), (12, 20) and (20, 100)
• The points (3, 10), (10, 20) and (20, 25).
• The points (4, 10), (10, 13) and (16, 16)

3.  Which of the graphs in #1 do you think has the same basic shape as that of pendulum period vs. length? 

Which of the graphs do you think has the same basic shape as that of pendulum frequency vs. length?

4.  Write down the equations we would get in each of the following situations.  You don't need to solve the equations at this point, and to solve some of the equations will in fact require that you use methods you probably don't know yet:

• We have y values 3, 9 and 21, which correspond to x values 8, 12 and 17, and we want to construct a generalized quadratic model.
• We have y values .7, 1.8 and 9.7 corresponding to x values 5, 10 and 15 and we want to construct a linear model.
• We have y values 2, 12 and 73 corresponding to x values 3, 9 and 13 and we want to construct an exponential function model.

5.  Multiplying or dividing both sides by the same quantity, adding the same quantity to both sides, raising both sides to the same power, etc., how do you solve each of the following for x?  Which of these equations cannot be solved for x using just these procedures?  Be sure you specify each step in each of your solutions..

• y = a x^2
• y = a sqrt(x)
• y = a ( x - h ) ^ 2 + k
• y = a x^2 + b x + c
• y = a / x^7

6.  Solve the system

• 2 a + 3 b = 8
• 5 a - 4 b = 2

for a and b, using the process of elimination.

7.  For pendulum period vs. length, if we obtain periods of .69, 1.08 and 1.41 seconds at lengths 12, 30 and 50 cm then the model T = a L^2 + b L + c gives us the three equations

• .69 = a * 12^2 + b * 12 + c
• 1.08 = a * 30^2 + b * 30 + c
• 1.41 = a * 50^2 + b * 50 + c

or

• .69 = a * 144 + b * 12 + c
• 1.08 = a * 900 + b * 30 + c
• 1.41 = a * 2500 + b * 50 + c

If we subtract the second equation from the first we eliminate c from the two equations, and if we subtract the third from the first we eliminate c from those two equations.  This gives us two equations

• -.39 = -756 a- 18 b  and
• -.72 = -2356 a - 38 b.

Solve these two equations for a and b, using the process of elimination.  Suggestion:  Start by eliminating b from the two equations.

Substitute your values of a, b and c into the form T = a L^2 + b L + c to get a quadratic model of T vs. L. 

• What period does your function predict if L = 40 cm?
• What period does your functin predict of L = 80 cm?

8.  Sketch a graph of T vs. L for the preceding data.

The correct T vs. L function is T = .2 sqrt(L). 

• What is the period T if L = 40 cm? 
• What is the period if L = 80 cm?

How does each of these period compare with the predictions of the quadratic model? 

• By how much does each differ from the quadratic model of #7?
• What percent of the correct result is each difference?

Laws of Exponents:

• x^a * x^b = x^(a+b)
• x^a / x^b = x^(a - b)
• x^(-a) = 1 / x^a.
• (x^a)^b = x^(a * b).