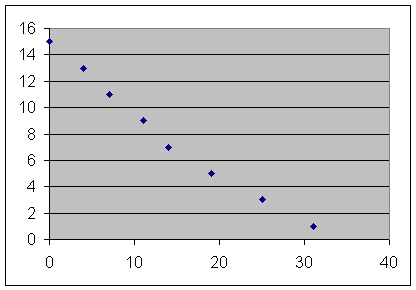
For depth vs. clock time observations:

• Make a table of position vs. clock time.
• Positions are 15 cm, 13 cm, 11 cm, ..., 1 cm.
• Clock time is the total time that has elapsed since the 15-cm mark.

Table, based on average of class observations:

Point graph of depth vs. clock time (note that depth is on vertical axis, clock time on horizontal, as dictated by the language 'depth vs. clock time')::

• Estimate the depths at clock times t = 5, 15 and 30 seconds.
• Put your estimates into the form y = a t^2 + b t + c to get three equations in three unknowns.

Your first equation will use t = 5.  If your depth estimate, based on a smooth curve thru the data points (NOT on actual data points), is y = 12 cm then the equation for this first point would be

12 = a * 5^2 + b*5 + c or

• 25 a + 5 b + c = 12.

If the estimate for the t = 15 depth is 6 cm then we get the equation

• 225 a + 15 b + c = 6.

Using estimated depth 1 cm for t = 30 sec we get the equation

• 900a + 30 b + c = 1.

We now have three simultaneous equations in a, b and c.

We can solve these equations for a, b and c by elimination.

The result is

• a = .0107
• b = -.813
• c = 15.8

Plugging these values into the form y = a t^2 + b t + c we get the model

• y = .0107 t^2 - .816 t + 15.8

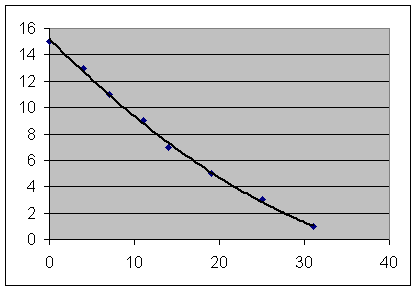
We can graph this equation using Excel, and we can then construct a scatter graph of y vs. t.  If we then right-click on a data point and choose Add Trendline, then choose a polynomial of degree 2 (and also click on Options > Display Equation of Graph), we will obtain a quadratic trendline with the 'best-fit' equation.

The Excel trendline gives us the model:

• y = 0.0062 t^2 - 0.6497 t + 15.21

Excel graph:

If the model is

• y  = 0.0062 t^2 - 0.6497 t + 15.21

then at what clock time will the depth be 10 cm?

Plug in 10 for y and you get

• 10  = 0.0062 t^2 - 0.6497 t + 15.21.

We will solve this equation using the Quadratic Formula.

Assignment:  Use the sheets handed out in class, or go to http://vhmthphy.vhcc.edu > Precalculus > Assts and look at Assignments 1 and 2 which give you links to the following:

• Read and think about Introduction to Central Themes; Examples

• Do Overview and Introduction:  The Modeling Process applied to Flow From a Cylinder

• Do Completion of the Introductory Flow Model , including the two exercises assigned at the end of that document.