Note that instructions for accessing a 'practice/quiz' program are given at the end of this page.

Quiz 0910

Do not use the graphing feature of your calculator to answer any of the following questions.

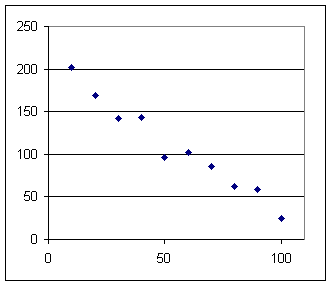
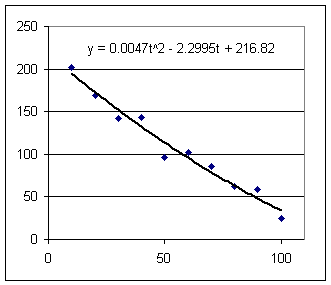
The quadratic model for the data shown below is y(t) = 0.0047t^2 - 2.2995t + 216.82.

1.  What is the prediction of the quadratic model for t = 70 and by how much does this prediction differ from the value observed for t = 70?

y(t) = 0.0047t^2 - 2.2995t + 216.82 so

y(70) = 0.0047 * 70^2 - 2.2995 * 70 + 216.82 = 78.9.

The t = 70 value for the graph appears to be about y = 85, which differs from the prediction by about 6 units.

This reflects the fact that the function model runs a bit below the data value for t = 70.

2.  Using the graph estimate the clock time at which the depth will be 120.

After sketching a good representative curve, sketch a line from the y = 120 point of the vertical axis to the curve, then project directly downward from this point. 

Your projection line will probably intersect the t axis in the neighborhood of t = 45, give or take a few.

3.  According to the model, at what clock time will the depth be 120?

The model is y(t) = 0.0047t^2 - 2.2995t + 216.82.

y(t) represents the depth, so the model predicts that the clock time is 120 when

120 = 0.0047t^2 - 2.2995t + 216.82.

This is an equation for t.  If we solve the equation to get t then we have answered our question.

How do we solve this equation for t?

First we recognize this as a quadratic equation.

Subtracting 120 from both sides gives us the equation

0.0047t^2 - 2.2995t + 96.82 = 0,

to which we can apply the quadratic formula, with a = .0047, b = -2.299 and c = 96.82.

We obtain two solutions, one for the + and the other for the - in front of sqrt(b^2-4ac).  Our two solutions are

t = 46.52997703  and t = 442.7253421.

The first of these solution corresponds to our situation.  The second is the solution we get when we extend the parabolic graph beyond vertex, which does not correspond to our depth vs. clock time situation.

4.  For the function y(t), what are the values of the following?

• y(40)

y(t) = 0.0047t^2 - 2.2995t + 216.82 so

y(40) = 0.0047* 40^2 - 2.2995 * 40 + 216.82 = 132.6

• y(a)

y(t) = 0.0047t^2 - 2.2995t + 216.82 so

y(a) = 0.0047* a^2 - 2.2995 * a + 216.82

• y(t+h)

y(t) = 0.0047t^2 - 2.2995t + 216.82 so

y(t+h) = 0.0047* (t+h)^2 - 2.2995 * (t+h) + 216.82

5.  For the function y(t), solve the equation y(t) = 150.

y(t) = 0.0047t^2 - 2.2995t + 216.82 so if y(t) = 150 we get

150 = 0.0047t^2 - 2.2995t + 216.82.

Subtracting 150 from both sides gives us the equation

0.0047t^2 - 2.2995t + 66.82 = 0,

to which we can apply the quadratic formula, with a = .0047, b = -2.299 and c = 66.82.

We obtain two solutions, one for the + and the other for the - in front of sqrt(b^x-4ac).  Our two solutions are

t = 458.2293228 and t = 31.02599630

6. The function indicates that y(20) =  172.7 and y(30) =152.1.  If y is depth in cm and t is clock time in seconds, then

• What do these two y values represent, and what to the two t values represent? 

These y values represent the depths in cm at clock times t = 20 sec and t = 30 sec.

• What is the change in y between t = 20 and t = 30?

y changes from 172.7 to 152.1, a change of (152.1 - 172.7) = -20.6, representing a depth change of -20.6 cm.

• What is the change in t between t = 20 and t = 30?

The change in t is (30 s - 20 s ) = 10 s.

• What do you get if you divide the change in y by the change in t and what does this quantity mean?

The change in y is -20.6 cm and the change in t is 10 sec, so

change in y / change in t = -20.6 cm / (10 sec) = -2.06 cm / sec.

Directions for Practice/Quiz Program.

This program is easy to use, once you've been through the process once.

If you are working at home you need only go through the download process once, and it's only a 1-step process to run the program. 

If you are working from VHCC you might have to go through the process each time you use the program, but it only takes a couple of minutes once you know what to do.  Once the network is properly set up there will be a version that runs much more conveniently from the LAN.

1. Go to Web address www.bb.vccs.edu and log in.  If you don't yet have your login name you can log in as vhstudent with password college.
2. Go to Supervised Study Current Semester (NOT to your Precalculus page) and Click on Course Documents.
3. At the top of the page is the program VBRUN60.  Run it (just one time) to be sure your computer is set up to run VB programs.  This is not necessary on VHCC computers.
4. Just below that is the program q_a_prelim.  Run it and as soon as it pops up, close it.  This program will create a folder entitled c:\vhmthphy on your hard drive.  Alternatively, if you prefer, you can create this file yourself.  If you are working on VHCC computers you will probably need to do this each time your run the program.
5. Scroll down that page until you see Multiple Choice Generating Program.  Either run the program or copy it to your desktop or some other location on your computer.  However don't answer any questions yet.
6. Just above that program on your Blackboard page you will find a link entitled Downloads.  Click on that link, then scroll down until you find the name of your course and click on that link.
7. At the bottom of the page for your course you will find the file 163_c.txt.  Right-click on that file, choose Save Target As..., browse your way into the folder C:\vhmthphy and save the program, without changing the name of the program.
8. Return to the Multiple Choice Generating Program.  Enter your VHCC username in the box where it is requested.
9. A form will pop up.  Click on the Menu button.
10. Enter 163 for your course number.
11. A list of topics will appear.  Enter the number of your choice.
12. Wait until a message pops up telling you how many questions you will have and OK that box.
13. The next box allows you to choose whether the questions will have just 1 correct answer or may have multiple correct answers.
14. Once you have answered this box the screen will tell you to click on the 'next question' button.  When you do a question will pop up.
15. Next you click on the Display Choices button and your choices will pop up.
16. Once you have decided which choice or choices are true you can click on the Answer Questions button.  Enter the letter(s) corresponding to the valid choice(s).
17. Click on the See Results button, which will give you (often repetitive) feedback on each of your answers.
18. Click on the Next Question button and repeat the process.

If you're working at home, once the 163_c.txt file is in the c:\vhmthphy folder and the program itself is on your desktop, you just need to double-click to run the program.

It will be equally easy at VHCC once the network is set up to accomodate the program.