0924

0927

change default page on each computer to http://vhmthphy.vhcc.edu

For reference: Synopsis with References to Multiple Choice

Path from Default Page: Precalculus I > Assts scroll to bottom of page then Partial Notes for Fall 2004

At the computer, use Windows Explorer to find h:\shares\physics and open the program Multiple Choice Questions. Using 163 as your course, run the following, in order, getting as far as you can.

Forms of the Basic and Generalized Basic Functions
Average rate of change of a quadratic.
Moving around the coordinate plane.
Stretching and shifting quadratics.
Very Basic Properties of Quadratic Functions
Graphs of Basic Functions

In addition to completing the worksheets distributed Friday do the following exercise, which will be the content of Wednesday's class:

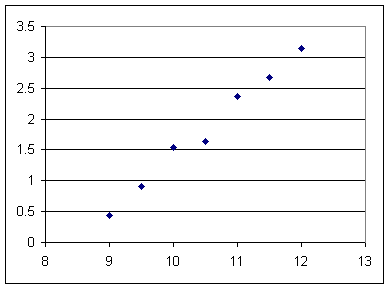
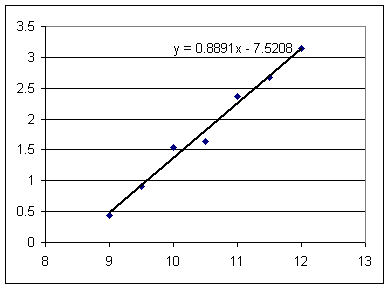
The graph below consists of a number of observations of the amount of weight in Newtons suspended from a rubber band vs. the length in cm of the rubber band. We can assume that there is some uncertainty in every observation, due either to user carelessness or to gremlins.

Sketch the line you think comes closest, on the average, to the given point. The line is unlikely, on the average, to pass through any of the given points.

Give the coordinates of the points at which your line passes into and out of the rectangle defined by the graph.

Find the slope of your line.

What are the units of the slope?

What could be the meaning of this slope?

Estimate from the graph of your straight line the weight of water that would extend the rubber band to length 10.3 cm.

Estimate from the graph of your straight line the length of the rubber band necessary to support a 3 Newton weight.

Substitute the coordinates of your two points into the generalized form y = m x + b of a linear function.

What two equations do you get?

Solve these equations for the parameters m and b.

Substitute the values of these parameters back into the generalized form to get your equation.

Solve the equation to determine the length of the rubber band necessary to support a 2 Newton weight.

Solve the equation to determine the weight of water that would extend the rubber band to length 12.5 cm

Do you think that the straight-line model is probably pretty accurate for this rubber band, in the sense that the actual weights supported at 9, 9.5, 10, 10.5, 11, 11.5 and 12 cm are probably closer to the values predicted by the straight line than to values predicted by the actual data points on the graph?

Is there any evidence that the behavior of the rubber band is not really linear?

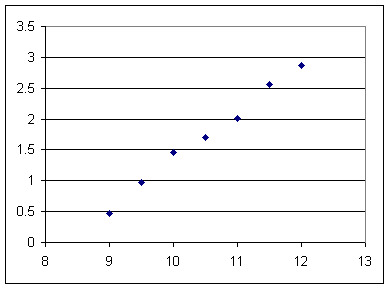
The graph below depicts similar data for another rubber band. Sketch your best-fit straight line.

Assume that there is some experimental error in these observations, but not nearly as much as in the previous graph. Does it appear that the actual behavior of this rubber band deviates in a significant manner from linear?

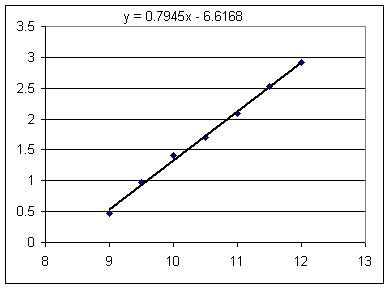
The graph below depicts another set of data for the same rubber band observed in the preceding graph.

Is there significant evidence that the behavior of this rubber band deviates at least slightly from linear?

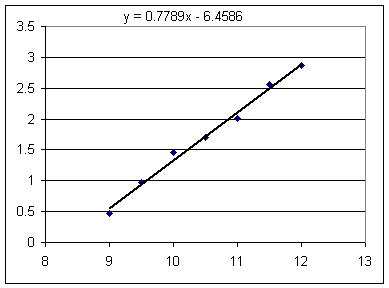
Sketch your 'best' straight-line model for the data in the preceding, then compare its slope with that of the model shown below by stating which has the greater slope, and by supporting your claim.

The basic linear function is y = x.

The graph of this function is a straight line characterized by a slope of 1 and a y-intercept y = 0.

If this basic function is vertically stretched by factor m, the line remains straight and its slope becomes m and y = m * x.
If the function is then vertically shifted through displacement b, every point is displaced y units in the vertical direction. Its y intercept thus becomes y = b and its formula becomes y(x) = m x + b.
To graph this function we can graph the point ( 0 , b ) on the y axis and the point 1 unit to the right of this point; this second point is displaced 1 unit horizontally and m units vertically from (0 , b).
A linear function will exactly fit any two given data points for which the horizontal coordinates differ.

Typical situations involving linear functions include

Force vs. displacement of pendulum
Horizontal range of stream vs. time for flow from side of vertical uniform cylinder
Income: Money earned vs. hours worked
Demand: Demand for a product vs. selling price (simplified economic model)
Straight-line approximation to any continuously changing quantity over a short time interval

We can form a good linear model of a set of data points by sketching a line which minimizes the average distance between the data points and the line.

We then choose two points on the line and plug them into the y = mx + b form of the equation of a straight line and determine the parameters m and b.

Given two points on a straight line we can use the slope = slope form ( y - y1) / ( x - x1) = slope, where slope = rise / run = ( y2 - y1) / ( x2 - x1).

It is essential understand the geometry and the logic of this form of the equation of a straight line.
Any equation in slope = slope form can be easily rearranged by solving for y to obtain the slope-intercept form.

The basic points on the graph of a linear function are taken to be the y-intercept and the point 1 unit to the right and m units up from this point.

For any function y = y(x), between x = x1 and x = x2 the linear function between the two corresponding graph points gives us an approximation of the original function.

For most functions when x1 and x2 are sufficiently close the approximation is also close to the actual function.

An equation of the form a(n+1) = a(n) + m, with an initial value a(0), generates a set of points which lie on the graph of a straight line whose slope is m and whose y intercept is a(0).

Problem Number 1

Problem: Obtain a quadratic depth vs. clock time model if depths of 67.39103 cm, 52.27462 cm and 42.65076 cm are observed at clock times t = 9.731353, 19.46271 and 29.19406 seconds.

This means to plug the numbers into the form of a quadratic and solve the 3 simultaneous equations for a, b, c; then plug the parameters a, b and c back into the model.

Problem: The quadratic depth vs. clock time model corresponding to depths of 67.39103 cm, 52.27462 cm and 42.65076 cm at clock times t = 9.731353, 19.46271 and 29.19406 seconds is depth(t) = .029 t² + -2.4 t + 88. Use the model to determine the clock time at which depth is 63.89874 cm.

depth(t) = .029 t² + -2.4 t + 88.

Find the clock time at which depth is 63.89874 cm.

Plug in 63.9 cm for depth(t) to get the equation

63.9 = .029 t² + -2.4 t + 88

and solve the equation (use the quadratic formula).

Problem Number 2

Problem: Sketch a graph of the basic exponential function y = 2^x. Sketch the graph of this function stretched vertically by factor -2.72 then shifted -1.78 units vertically. Show that the graph is different than that obtained if the vertical shift precedes the vertical stretch. Give the algebraic form of the resulting function.

Vertical stretch by factor -2.72 multiplies all y values by -2.72, making the function y = -2.72 * 2^x.

Use basic points like (-1, 1/2), (0, 1) and (1, 2) to sketch a picture of the graph then vertically stretch each point, and use these points as a basis for your new graph.

Vertical shift -1.78 lowers each point 1.78 units, giving us the function y = -2.72 * 2^x - 1.78.

Problem: At clock times t = 6, 12, 18 and 24 seconds, the depth of water in a uniform cylinder was observed to be 34.336, 30.544, 28.624 and 28.576 cm. At what average rate was the depth changing during each of the three time intervals?

For each interval calculate change in depth / change in clock time, corresponding to rise / run of the graph.

There are 3 intervals and you need to calculate for each, meaning you'll calculate 3 rates.

Look at the rates you have calculated and predict what the next average rate would be. If your prediction is correct, then what will be the depth at t = 30 seconds?

There will be a pattern to these rates and it will be easy to predict the next rate.

Then using the rate you can calculate the change in depth over the next 6-second interval.

Problem Number 3

Sketch a graph of y = x^2, from x = -3 to x = 3. Then sketch a graph of y = 4 x^2 over the same domain.

By what factor do we vertically stretch the first graph to obtain the second?
What are the three basic points of the first graph (i.e., the vertex and the points 1 unit to the right and left of the vertex)?
What are the three basic points of the second graph?

Sketch the second graph shifted -.25 units in the x direction and -1.25 units in the y direction.

What are the three basic points of this graph?

If f(x) = x^2, then what are

f(x--.25),
f(x) + -1.25,
4 f(x) and
4 f(x--.25) + -1.25?

and what are the basic points of each?

f(x - -.25) gives us (x - -.25)^2 = (x + .25)^2, which shifts the graph -.25 units in the horizontal direction, giving basic points (-1.25,1), (-.25, 0) and (.75, 1).

f(x) + -1.25 gives us x^2 - 1.25, which shifts the y=x^2 graph vertically -1.25 units, giving us basic points (1, -.25), (0, -1.25) and (1, -.25).

etc.

Problem Number 4

Make tables and sketch graphs of the power functions y = x² , y = x³ , y = x^-2 and y = x^-3 , for x = -3 to 3.

Show what happens to each graph if it is vertically stretched by factor 2.

Problem Number 5

If water depths of 63.7, 56.3, 52.2 and 51.3 cm are observed at clock times 14.6, 21.9, 29.2 and 36.5 sec, then at what average rate does the depth change during each time interval?

This is as before.

Sketch a graph of this data set and use a sketch to explain why the slope of this graph between 21.9 and 29.2 sec represents the average rate at which depth changes during this time interval.

Here you need to sketch the graph, explain what the rise between the two points means, what the run means, and what the slope therefore means.

If f(x) = x², give the vertex and the three basic points of the graphs of f(x--.25), f(x) - 1.85, 2 f(x) and 2 f(x--.25) + 1.85. Quickly sketch each graph.

Completely analogous to the above.