1101

• Run Multiple Choice Generator at h:\shares\physics
• Run Core Problems by giving the program 174 as your 'course'--enter this when asked for your 3-digit course number.  
• Do the 'quiz' on Exponential Functions
• If you miss a problem be sure to click on Comment and explain what you do and do not understand about the question and the given solution

What is the equation for the doubling time of an exponential principle function if the interest rate is r?

What is the principle function?

• This would be the function which corresponds to continuous compounding at annual rate r.
• The function is P(t) = P0 e^(r t).

What therefore is the equation for the doubling time?

• Principle at t = 0 is P0.  So principle doubles when P(t) = 2 * P0.
• The equation for doubling time, using t_doub for doubling time, is therefore P(t_doub) = 2 * P0, or
• P0 e^( r * t_doub) = 2 * P0, which simplifies to
• e^(r * t_doub) = 2.

If we have exponential growth with growth rate r, then what is the equation for doubling time?

If growth rate is r, then growth factor is 1 + r and our exponential function is

• Q(t) = Q0 ( 1 + r ) ^ t. 

(The paradigm situation is annual interest rate r with annual compounding).

The quantity Q(t) doubles from its initial amount in the time necessary for Q to increase to twice its initial amount.  The initial amount is Q0 so if the doubling time is t_doub we have

• Q(t_doub) =

  Q0 ( 1 + r)^t_doub = 2 * Q0,

giving us the equation

• Q0 ( 1 + r)^t_doub = 2 * Q0,

which we simplify to get just

• ( 1 + r)^t_doub = 2 .

How can we use graphs to get doubling time?

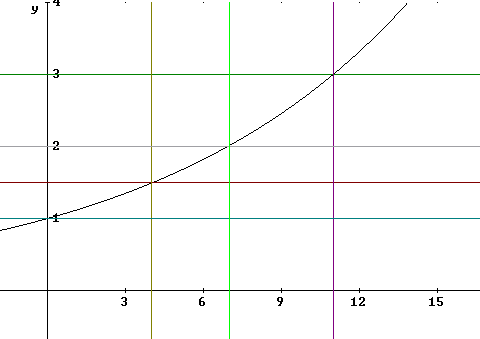
We can sketch two horizontal lines, one twice as far from the t axis as the other.  Look at the y = 1.5 and y = 3 lines below.

These lines cross the graph at points between which the y value doubles.

If we project these graph points to the t axis we will have the two clock times between which the y value doubles.

The points for the y = 1.5 and y = 3 lines lie at t = 4 and t = 11.  So the doubling time is `t_doub = 11 - 4 = 7.

The graph also shows the y = 1 and y = 2 lines.  The same process again leads to doubling time 7.

The function shown is an exponential function with horizontal asymptote t = 0.  The doubling time is always the same for such an exponential function.  This is not true of any other type of function.  If doubling time is always the same, the function is an exponential function.

What are the basic points of the graph of the exponential function shown in the picture?

The basic points are the t = 0 and t = 1 points.

The t = 0 point is (0, 1) and the t = 1 point appears to be (1, 1.1) (we sketched the line t = 1 and then estimated that y = 1.1; the line y = 1.1 appears to be about right). 

The graph (with the scale changed so we can see what's happening) is below:

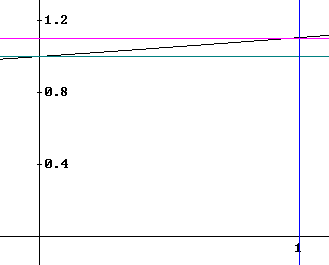
What therefore is the function?

The basic points of y = A b^t are the

• t = 0 point, where y = A b^0 = A * 1 = A and
• the t = 1 point, where y = A b^1 = A * b.

The identified points are

• the t = 0 point (0, 1), which implies that A = 1 and
• the t = 1 point (0, 1.1), which implies that A * b = 1.1.  Since A = 1, this gives us b = 1.1.

The function is therefore y = 1 * 1.1^t, or just y = 1.1^t.