1112

• Run Multiple Choice Generator at h:\shares\physics
• Run Core Problems by giving the program 174 as your 'course'--enter this when asked for your 3-digit course number.  
• Do the 'quizzes' on Exponential Functions: Numbers and Exponential Functions: Graphs.
• If you miss a problem be sure to click on Comment and explain what you do and do not understand about the question and the given solution

http://www.vhcc.edu/dsmith/images/graph_series_1.htm

• Pendulum data: 

Length	Period	log(length)	log(period)
5	0.4	0.699	-0.398
15	0.7	1.1761	-0.155
35	1.2	1.5441	0.079
60	1.5	1.7782	0.176

Graph period vs. length, log(period) vs. log(length), period vs. log(length) and log(period) vs. length.

Is any of these graphs linear?

T vs. L isn't linear.

log(T) vs. L isn't linear.

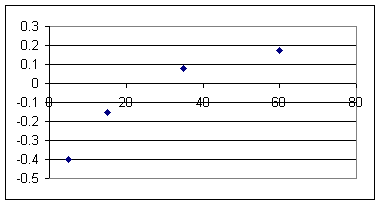
log(T) vs. log(L) is very nearly linear.

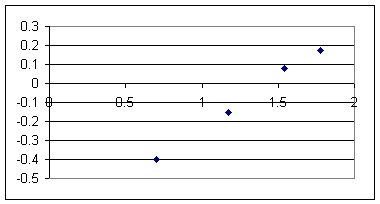
Slope of log(T) vs. log(L) is about .55 and y-intercept is close to -.9 (rough estimates).

So our equation is log(T) = .55 log(L) - .9.

Solving for T we get

10^log(T) = 10^(.55 log(L) - .8)

T = 10^-.8 * L^.55 or

T = .16 L^.55.

For what values of x is the function

• y = (x - 4) (x + 7)

equal to zero?

If x = 4, then x - 4 is zero so the product (x-4)(x+7) is zero.

If x = -7, then x + 7 is zero so the product (x-4)(x+7) is zero.

Are there any other values of x for which y = 0?

When we plug in we get two numbers, which we're gonna multiply.  If one of those numbers isn't zero, we aren't gonna get zero for the product.

The only numbers that give us zero are therefore x = 4 and x = -7.

What does this tell us about the graph of y vs. x?

This tells us that the only points where the graph crosses the x axis are (-7, 0) and (0, 4).

What is the y-intercept of the graph of y = (x-4)(x+7)?

The graph crosses the y axis at the point where x = 0.

At this point we have y = (0 - 4) ( 0 + 7) = -28.

So the y intercept is (0, -28).

If x is a great bit huge humongous number, what can we say about the value of y?

y = (x-4)(x+7).  If x is really huge, then x - 4 and x + 7 will both be really huge.  So when we multiply them the result will be a really, really huge number.

What does this tell us about the graph?

It tells us that if we go far to the right, the graph gets really, really high.

Starting with

• log(y) = 5 log(x) + 7 we take apply the inverse function 10^x to both sides to obtain
• 10^log(y) = 10^(5 log(x) + 7). 

The left-hand side is just y; using the laws of exponents on the right-hand side we get

• y = 10^(5 log(x) ) * 10^7. 

Since 10^(ab) = (10^a)^b the factor 10^(5 log(x)) = (10^(log(x))^5) so

• y = ( 10^log(x) ) ^ 5 * 10^7.  Since 10^log(x) = x we have
• y = 10^7 * x^5.

So y is a power function of form y = A x^p with A = 10^7 and p = 5.

• Solve the equation log(y) = 5 x + 7.  What sort of function is y(x)?

Starting with

• log(y) = 5 x + 7 we take apply the inverse function 10^x to both sides to obtain
• 10^(log(y)) )= 10^(5x + 7).

The left-hand side is just y; using the laws of exponents on the right-hand side we get

• y = 10^(5x) * 10^7.

Since 10^(ab) = (10^a)^b the factor 10^(5 x) = (10^5)^x so

• y = 10^7 * (10^5)^x = 10^7 * 100,000^x.

This function is an exponential function of form y = A b^x with A = 10^7 and b = 100,000.

Generalizing:

If

• log(y) = m log(x) + b

then when we solve for y we get a power function.

If

• log(y) = m x + b

then when we solve for y we get an exponential function.

If we have a table of y vs. x data, then if a graph of log(y) vs. log(x) gives us a straight line, we can find the slope m and the y-intercept b and get the equation log(y) = m log(x) + b.

Of a graph of log(y) vs. x is linear, then the slope and y intercept will give us the form log(y) = m x + b.