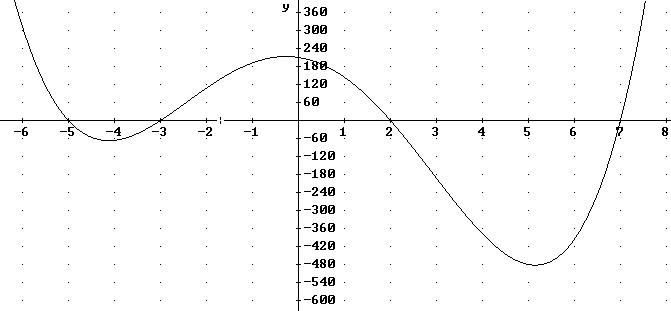
1117

• Run Multiple Choice Generator at h:\shares\physics
• Run Core Problems by giving the program 174 as your 'course'--enter this when asked for your 3-digit course number.  
• Do the 'quizzes' on Exponential Functions: Numbers and Exponential Functions: Graphs.
• If you miss a problem be sure to click on Comment and explain what you do and do not understand about the question and the given solution

http://www.vhcc.edu/dsmith/images/graph_series_1.htm

Construct the graph of y = p(x) = (x - 2) ( x + 3) * (x - 7) ( x + 5).

We know that the x intercepts must be at x = -5, -3, 2 and 7.

The y-intercept is at p(0) = -2 * 3 * -7 * 5 = 210.

At far left x is a large negative, which gives us the product of four large negatives, which is a large positive.

At far right x is a large positive, which gives us the product of four large positives, which is a large positive.

So we get the graph

Construct the graph of

• y = (x - 2)^2 ( x + 3)^3 * (x - 7) ( x + 5).

We know that the x intercepts must be at x = -5, -3, 2 and 7.

The y-intercept is at p(0) = (-2)^2 * 3^3 * -7 * 5 = -3780.

At far left x is a large negative, so every linear factor is a large negative.  This gives us the product of the square of a large negative, the cube of a large negative, and two other large negatives.  This is the product of a total of 7 large negative numbers, which gives us a huge negative number.

At far right x is a large positive, which by similar reasoning gives us the product of seven large positives, which is a huge positive.

Our graph has to start out at a large negative and end up at a large positive, going through only the zeros we've listed (no other number can possibly give us zero, since none of the factors would be zero), and going through the y intercept.

Seems like we CAIN'T do it.  We end up below the x axis having to get back to large positives, but we don't have another zero to go through.

Gotta think about this.

Think about what happens when x is close to 2.

We have (x-2)^2 ( x+3)^3 (x-7) (x+5).  When x is close to 2, (x - 2) could be positive or negative depending on whether x is a little less than 2 or a little greater.  However x+3 is close to 5, x - 7 is close to -2 and x + 5 is close to 7, and none of these values changes significantly as long as x stays close to 2.

So the product is close to (x-2)^2 * 5^3 * (-5) * 7 = -4377 so our function is close to

• -4377 ( x - 2)^2 (close to our original function if x is close to 2)

This is just our basic quadratic y = x^2, vertically stretched by factor 4377 and horizontally shifted 2 units.

Give the formula for a polynomial function which passes through the points (-3, 0), (2, 0) and (5, 0), having a y-intercept of 4.

Sketch graphs of f(x) = (x - 3) and g(x) = (x+ 2).

• Identify the points on the x axis at which either f(x) = 0 or g(x) = 0.
• Identify the points on the x axis at which either | f(x) | = 1 or | g(x) | = 1.
• Identify the interval(s) of the x axis over which | f(x) | < 0.
• Identify the interval(s) of the x axis over which | g(x) | < 0.
• Identify the interval(s) of the x axis over which | f(x) | < 1.
• Identify the interval(s) of the x axis over which | g(x) | < 1.
• Identify the point(s) of the x axis for which f(x) = - g(x).

For the functions f(x) and g(x) of the preceding problem

• If f(x) = 0 then what is the value of the function f(x) + g(x)?
• If g(x) = 0 then what is the value of the function f(x) + g(x)?
• If f(x) = - g(x) then what is the value of the function f(x) + g(x)?
• If f(x) < 0 then what is the value of the function f(x) + g(x)?
• If f(x) > 0 then what is the value of the function f(x) + g(x)?
• Can you use this information to construct a graph of f(x) + g(x)?

For the functions f(x) and g(x) of the preceding problem

• If f(x) = 0 then what is the value of the function f(x) * g(x)?
• If g(x) = 0 then what is the value of the function f(x) * g(x)?
• If f(x) = 1 then what is the value of the function f(x) * g(x)?
• If g(x) = 1 then what is the value of the function f(x) * g(x)?
• If f(x) < 0 then what can we say about the value of the function f(x) * g(x)?
• If g(x) < 0 then what is the value of the function f(x) * g(x)?
• If f(x) < 0 and g(x) < 0 then what can we say about the value of g(x)?
• If f(x) < 0 and g(x) > 0 then what can we say about the value of g(x)?
• If f(x) > 0 and g(x) < 0 then what can we say about the value of g(x)?
• If f(x) > 0 and g(x) > 0 then what can we say about the value of g(x)?
• If | f(x)| = 1 then what is the value of the function f(x) * g(x)?
• If | g(x)| = 1 then what is the value of the function f(x) * g(x)?