http://www.vhcc.edu/pc1fall9/gov03/
For explanations on Trapezoidal Graph quizzes: http://www.vhcc.edu/cal1fall/classes_2002/notes_from_fall_02_classes.htm
09:40:36
Go to the address http://www.vhcc.edu/ph2spring99/experiments/kinetic_model.htm
(copy and paste this address into the Address box of your browser). Click on the
link KINMODEL and choose the default settings with medium speed. You'll know
what to do when you see those prompts. Observe the red ball to a couple of
minutes and get a feel for the fastest speed at which you've seen the ball
travel, and for the slowest. (The model may be paused by pressing the
pause-break key (top right on the keyboard) or by striking the letter s).
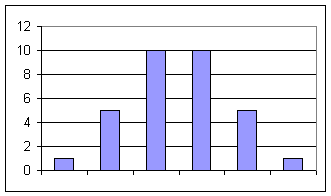
Assuming the fastest speed is 12 and the slowest is 1 decide what percent of its
time the ball appears to spend in each of the six speed ranges 1-2, 3-4, 5-6,
7-8, 9-10, and 11-12. Give your percents. Sketch a bar graph representing your
estimates.
......!!!!!!!!...................................
RESPONSE -->
Speed range: Percent:
1-2 7%
3-4 15%
5-6 34%
7-8 31%
9-10 8%
11-12 5%
** these percents add up to more than 100%. That just
cain't be. **
Since I didn't understand the question or how to find the answers, I don't think
I can answer this question. I understand what to do in this question, but I
don't have the information needed to answer this.
.................................................
......!!!!!!!!...................................
09:45:12
Using your estimates from the preceding question give your estimate of the
average speed of the red ball, which you will calculate as follows: Multiply the
middle of each speed range by the percent, except express the percent as a
decimal. For example if you estimated that ball was in the speed range 1-2 about
80% of the time then you would multiply the midpoint of the 1-2 range by .80.
The midpoint of that range is halfway between 1 and 2, or 1.5, so you would
multiply .80 * 1.5. Add up your results. This is your average speed. Give your
results and explain why you think this should represent the average speed.
......!!!!!!!!...................................
RESPONSE -->
The avgerage speed is calculated using this equation:
(1.5*.07)+(3.5*.15)+(5.5*.34)+(7.5*.31)+(9.5*.08)+(11.5*.05) = 6.16
** since the percents add up to more than 100% this is gonna be a little more than the correct average. **
I think this should give me avg. speed because it calculates how long the ball
was in each speed range.
.................................................
......!!!!!!!!...................................
09:50:17
You will now find the root-mean-square of your results. This time you will
multiply the percent by the square of the middle of each speed range, add up
these results, and then take the square root of this sum. What do you get? Why
do we call this the root-mean-square? Any idea why this should be a significant
quantity?
......!!!!!!!!...................................
RESPONSE -->
I obtained 4.4763 as my root-mean-square. If I had to guess, I would say the
name comes from squaring the avg. (or mean) and once all of them are added
together, taking the root. However, I have no idea why this quantity is
significant.
(1.5^2*.07)+(3.5^2*.15)+(5.5^2*.34)+(7.5^2*.31)+(9.5^2*.08)+(11.5^2*.05)
** Find the sum of all these products and take the square root to get the root-mean-square **
.................................................
......!!!!!!!!...................................
09:57:43
Pick a number between 0 and 1. Don't pick anything obvious like 0, .5 or 1. Call
this number x. Figure out the number 3 x * ( 1 - x). Call this number x. Figure
out the number 3 x * ( 1 - x). Call this number x. Figure out the number 3 x * (
1 - x). Continue this process until you have ten numbers and give the results.
Is there any pattern to your results?
......!!!!!!!!...................................
RESPONSE -->
x = .3
3x * (1 - x)
3 (.3) * (1-.3)
.9 * (.7)
.63
x = .63
3 (.63) * (1 - .63)
1.89 * (.37)
.6993
x = .6993
3 (.6993) * (1 - .6993)
2.0979 * .3007
x = .63083853 (x = .63)
x = .63083853
3 (.63083853) * (1 - .63083853)
1.89 * .369
.6986
x =.6986
3 (.6986) * (1 - .6986)
2.09 * .301
.63
x = .63
3 (.63) * (1 - .63)
1.89 * .3684
.698
x = .698
3 (.698) * (1 - .698)
2.09 * .301
.63
x = .63
3 (.63 ) * (1 - .63)
1. 89 * .3676
.69
x = .69
3 (.69) * (1 - .69)
2.09 * (.3025
.63
x= .63
3 ( .63) * (1 - .63)
1.89 * .3677
.69
Final results: .63, .69, .63, .69, .63, .69, .63, .69, .63, .69
The pattern is obvious. .63, .69, .63, .69 etc.
There is a slight pattern, if you would call it that, where-in after the pattern
really gets going, the numbers increase, then decrease, then increase, then
decrease. This pattern continues until the end after the 2nd number.
** The numbers bounce up and down but gradually get closer and closer together.
This map, where x is repeatedly replace by 3 x ( 1 - x), is called a logistic map.
The general form of a logistic map is m x ( 1 - x), where m is a number between 0 and 4.
Repeat this exercise for m = 1 (i.e., using 1 * x * (1-x)) and for m = 2.
Then try m = 3.99.
The closer m is to 4 the more unpredictable our results will be. **
ok, for my fisrt number I chose 2.
So, 3*2(1-2)=-6
Now my x number is -6
So, 3*(-6)*(1-(-6))=-12
Now my x number is -12
So, 3*(-12)*(1-(-12))=-24
Now my x number is -24
So, 3*(-24)*(1-(-24))=-48
Now my x number is -48
So, 3*(-48)*(1-(-24))=-96
Now my x number is -96
So, 3*(-96)*(1-(-96))=-192
Now my x number is -192
So, 3*(-192)*(1-(-192))=-384
Now my x number is -384
So, 3*(-384)*(1-(-384))=-768
Now my x number is -768
So, 3*(-768)*(1-(-768))=-1536
Now my x number is -1536
So, 3*(-1536)*(1-(-1536))=-3072
** note that if x isn't between 0 and 1 the result 'blows up'. **
.................................................
......!!!!!!!!...................................
10:01:47
Find the mean of the numbers in the n = 5 row of Pascal's Triangle. The numbers
in that row are 1, 5, 10, 10, 5 and 1, standing for the numbers of ways to get
0, 1, 2, 3, 4 and 5 Heads. To find the mean first add up all the possible
outcomes (i.e., add up the row). Then multiply each number of Heads by the
number of ways in which it can happen. Add up your results and divide by what
you got when you added up the row. What did you get, why does it make sense and
why does this work?
......!!!!!!!!...................................
RESPONSE -->
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1+5+10+10+5+10=32
1*0=0
5*1=5
10*2=20
10*3=30
5*4=20
1*5=5
0+5+20+30+20+5=80
80/32=2.5 Avg mean
I do not know why this works and does not make much sense to me.
When I divided, I received an answer of 2.5, whcih makes sense because that is
the avg. of the first and last number of heads (i.e. 0 and 5).
** Note that if you make a histogram of the number of ways you can get different numbers of Heads the graph is symmetric about n = 2.5.
In the figure the numbers of Heads n = 0, 1, 2, 3, 4, 5; there is a bar for each number.

**
.................................................
......!!!!!!!!...................................
10:03:04
Suppose that you have water flowing into a container at 100 cm^3 / second. If
the cross-sectional area of the container is 20 cm^2 then at what rate will
water be rising in the container?
......!!!!!!!!...................................
RESPONSE -->
** To get the rate at which water rises we divide the number of cm^3 per second by the cross-sectional area.
At 100 cm^3 / second water will rise in a 20 cm^2 tube at 100 cm^3/second / (20 cm^2) = 5 cm/s. **
.................................................
......!!!!!!!!...................................
10:12:18
Suppose you have water flowing into a container at 100 cm^3 / second. If the
cross-sectional area of the container at depth y, in cm, is 10 cm^2 * y then at
what rate will the water be rising when y = 5 cm? At what rate will the water be
rising when y = 10 cm? At what rate will the water be rising when y = 15 cm?
Estimate the time required for the water to rise from 5 cm to 10 cm, and from 10
cm to 15 cm.
......!!!!!!!!...................................
RESPONSE -->
At y = 5 cm the area is 10 cm^2 * 5 = 50 cm^2.
So water is rising at the rate 100 cm^3 / (50 cm^2) = 2 cm / s
At y = 10 cm the area is 10 cm^2 * 10 = 100 cm^2.
So water is rising at the rate 100 cm^3 / (100 cm^2) = 1 cm / s
At y = 15 cm the area is 10 cm^2 * 15 = 150 cm^2.
So water is rising at the rate 100 cm^3 / (50 cm^2) = .66... cm / s
Between y = 5 cm and y = 10 cm the rate of change of depth changes from 2 cm/s to 1 cm/s so the average rate of change of depth is about 1.5 cm/s.
At this average rate the water will require
change in depth / rate = 5 cm / (1.5 cm/s) = 3.33... sec to rise the 5 cm from y = 5 cm to y = 10 cm.
Between y = 10 cm and y = 15 cm the rate of change of depth changes from 1 cm/s to .666.. cm/s so the average rate of change of depth is about .833.. cm/s.
At this average rate the water will require
change in depth / rate = 5 cm / (.833.. cm/s) = 6 sec to rise the 5 cm from y = 10 cm to y = 15 cm.
ANOTHER SOLUTION:
To get this, you must divide your answer after sub. in "y" into 100cm^3/sec.
y=5----->2cm/sec
y=10--->1cm/sec
y=15--->0.666......cm/sec
To do the last part, I may be wrong, but I believe you avg. the two rates for
the depths desired and divide that into the overall "flow-in" rate.
.................................................
......!!!!!!!!...................................
10:17:15
Suppose you have water flowing into a container at 100 cm^3 / second. If the
cross-sectional area of the container at depth y, in cm, is 10 cm^2 * y then at
what rate will the water be rising when y = 5 cm? If this rate continued for 2
seconds what would then be the water level at the end of this time? At what rate
would water be rising at this new level, and if this rate continued for another
2 seconds what would then be the water level at the end of this time? At what
rate would water be rising at this new level, and if this rate continued for
another 2 seconds what would then be the water level at the end of this time?
......!!!!!!!!...................................
RESPONSE -->
WELL ORGANIZED SOLUTION; RATE IS CALCULATED UPSIDE DOWN.
y = 5: 10cm^2(5) = 50 cm^2
rate = 50cm^2/100cm^3/second
** You need to divide the rate of volume flow by the cross-sectional area, not
the other way around **
rate = 0.5 cm/second
y = 10: 10 cm^2(10) = 100 cm^2
rate = 100 cm^2/100 cm^3/second
rate = 1 cm/second
y= 15: 10 cm^2(15) = 150 cm^2
rate = 150 cm^2/100 cm^3/second
rate = 1.5 cm/second
5 - 10: 10 seconds
10 - 15: 5 seconds
** good work except for the reversal in calculating rate of depth change **
GOOD SOLUTION WITH NARRATIVE DETAILS
The rate at a depth of 5cm would be 100cm^3 / s divided by 50cm^2, or 2cm^3/s.
If this continued for 2 secs, then the new level would be 9cm.
The rate at a depth of 9cm would be 100cm^3 / s divided by 90cm^2, or 1.1cm^3/s.
If this continued for 2 secs, then the new level would be 11.2cm.
The rate at this depth would be 100cm^3/s. The area would be
area = 10 cm^2 * y = 10 cm^2 * 11.2 = 112 cm
so the rate of depth change would be the 100 cm^3 / sec flow
rate divided by 112cm^2, or 0.89cm^3/s. If
this continued for 2 secs, then the new level would be 12.98cm.
ANOTHER SOLUTION
Water would rise at 2cm/sec at y=5. If this rate continues for 2sec, the water
lvl would be 9cm. The new rate would be 1.1111111cm/sec. After 2sec, the water
lvl would be 11.222cm. The new rate would then be 0.891cm/sec. After 2sec, the
new lvl would be 13.004cm.
.................................................
......!!!!!!!!...................................
10:22:54
Trace out the first 5 steps of the Christmas Tree problem whose rule is that a
tree becomes lit provided exactly one of the three trees (the tree itself or one
of its neighbors) is lit or the tree and its neighbor to the right but not the
neighor to the left are both lit. Start with a row of 11 trees (not in a circle)
with all trees off except the one in the middle. Use 0's and 1's for 'on' and
'off' trees.
......!!!!!!!!...................................
RESPONSE -->
100 or 010 or 001 or 011 light the tree in the next step
0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 1 1 1 0 0 0 0
0 0 0 1 1 0 0 1 0 0 0
0 0 1 1 0 0 1 0 1 0 0
0 1 1 0 1 1 1 0 1 1 0
1 1 0 0 1 0 0 0 1 0 1
1 1 1 1 1 0 1 1 1 1 1
1 1 1 1 0 1 0 1 1 1 1
1 1 1 0 1 0 1 0 1 1 1
1 1 0 1 1 1 1 1 0 1 1
1 0 1 1 1 1 1 1 1 0 1
I'm not sure if this is exactly correct.
.................................................
......!!!!!!!!...................................
10:48:35
Find on the Governor's School homepage the link to Trapezoidal Graph
Interpretation and click on that link. Answer the questions in Quizzes 1, 2 and
3.
......!!!!!!!!...................................
RESPONSE -->
CHECK TO SEE IF THESE RESPONSES ARE CORRECT
Quiz 1--->3.625gal/hr; the number of gallons in the bucket after 1.5hrs; 1.5 is
the number of hrs. since the start of the rain; 3cm/sec; 0.75cm; 3.75cm; the
rate at which the rate is changing between 1 and 1.5min.
Quiz 2--->alt-$ in bank, slope-rate of increase, width-time in bank, area is the
money made during the interval, accum area is the money over the entire time;
alt-$ change=2.625, slope-change of the rate= 1.5, width- time in bank= .5 - 1
months, area - ??, accum area -??; alt- cs area, slope- change of cs area over
height above floor measured, width- height above floor that container measured
at, area- total change of the container over the width, accum area- total change
over the entire measuring
Quiz 3--->alt- avg. height= vel. of 5.125cm/sec, slope- avg. change of vel.=
3.5cm/sec/sec, width- time interval= 1.5-2sec, area is the total distance
traveled in the interval, accum area is the total distance during the entire
time
.................................................
Rule: Cell turns on if exactly one neighbor is on.
| left | cell | right | cell on/off | value | added to total |
| 0 | 0 | 0 | 2^0=1 | ||
| 0 | 0 | 1 | 2^1=2 | ||
| 0 | 1 | 0 | 2^2=4 | ||
| 0 | 1 | 1 | 2^3=8 | ||
| 1 | 0 | 0 | 2^4=16 | ||
| 1 | 0 | 1 | 2^5=32 | ||
| 1 | 1 | 0 | 2^6=64 | ||
| 1 | 1 | 1 | 2^7=128 |
Rule: exactly one of the three trees (the tree itself or one of its neighbors) is lit or the tree and its neighbor to the right but not the neighbor to the left are both lit.
| left | cell | right | cell on/off | value | added to total |
| 0 | 0 | 0 | 2^0=1 | ||
| 0 | 0 | 1 | 2^1=2 | ||
| 0 | 1 | 0 | 2^2=4 | ||
| 0 | 1 | 1 | 2^3=8 | ||
| 1 | 0 | 0 | 2^4=16 | ||
| 1 | 0 | 1 | 2^5=32 | ||
| 1 | 1 | 0 | 2^6=64 | ||
| 1 | 1 | 1 | 2^7=128 |
Rule number is 30.
| left | cell | right | cell on/off | value | added to total |
| 0 | 0 | 0 | 2^0=1 | ||
| 0 | 0 | 1 | 2^1=2 | ||
| 0 | 1 | 0 | 2^2=4 | ||
| 0 | 1 | 1 | 2^3=8 | ||
| 1 | 0 | 0 | 2^4=16 | ||
| 1 | 0 | 1 | 2^5=32 | ||
| 1 | 1 | 0 | 2^6=64 | ||
| 1 | 1 | 1 | 2^7=128 |
Rule number is 55
| left | cell | right | cell on/off | value | added to total |
| 0 | 0 | 0 | 2^0=1 | ||
| 0 | 0 | 1 | 2^1=2 | ||
| 0 | 1 | 0 | 2^2=4 | ||
| 0 | 1 | 1 | 2^3=8 | ||
| 1 | 0 | 0 | 2^4=16 | ||
| 1 | 0 | 1 | 2^5=32 | ||
| 1 | 1 | 0 | 2^6=64 | ||
| 1 | 1 | 1 | 2^7=128 |