| Rates | Areas, Volumes, etc. | Flows |
1. If you make new friends at an average of four friends / day then how many new friends do you make in 7 days?
2. If you travel at an average speed of 12 miles / hour then how long does it take you to travel 36 miles?
3. If you make 48 dollars in 6 hours then at what rate, in dollars / hour, are you making money?
4. On a graph of Q = amount of money in your pocket vs. t = number of hours since arriving at an arcade:
· What are the coordinates of the point which represents having $38 after 2 hours in the arcade?
· What are the coordinates of the point which represents having $3 after 5 hours in the arcade?
· Between t = 2 hours and t = 5 hours at what average rate was the amount of money in your pocket changing?
· Sketch a line segment from the first point to the second.
· What is the rise of the line segment?
· What is its run?
· What therefore is its slope?
· What does the slope of your graph of Q vs. t represent?
5. On the graph shown below of Q = amount of water in a container, in liters, vs. t = time in minutes since a hole developed in the container:
· Estimate the amount of water at t = 20 minutes and the amount at t = 50 minues.
· At what average rate is the amount of water changing, with respect to clock time t, between t = 20 minutes and t = 50 minutes?
· If the amount continued to change at this average rate for the next 10 minutes how much change would there be?
· How much change is there, according to the graph, in the next 10 minutes?
· How long would it take to change by this much at the average rate you calculated?
· What is the average rate over that 10-minute period?
Note the following definition: Average rate of change of y with respect to t between two graph points is
· Average rate = change in y / change in t
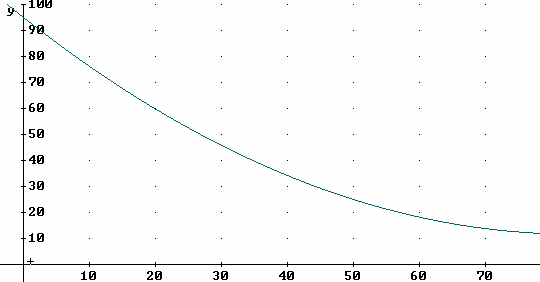
6. If we have 50 gallons of water in a container at a certain time, and if for the next 10 minutes the amount changes by +3 gallons / minute, then what will be the amount of water in the container at the end of that 10-minute period?
7. At a certain instant the speed of an object is 40 miles / hour and the speed is changing at the contant rate of 5 miles/hour per second. What was the speed of the object 5 seconds earlier?
8. If a growing animal weighs 200 lbs at a certain time, and 4 months later weighs 360 lbs, then at what average rate is the weight of the animal changing?
9. If the depth of water in a container is changing at a constant rate of 4 cm / sec then how long does it take for the depth to change from 40 cm to 60 cm?
10. Sketch a graph of Q vs. P to solve the following:
· Q = heart rate in beats / minute (abbreviated bpm) vs. P = work rate in watts.
· At a work rate of 300 watts the heart rate is 150 bpm.
· The rate at which heart rate changes with respect to work rate is .25 bpm / watt.
What therefore is the heart rate when the work rate is 400 watts?
11. On the graph below of Q = grade average vs. x = number of hours spent studying per week, sketch the point corresponding to grade average 2.4 being obtained by studying 12 hours / week. Sketch a horizontal line representing grade average 3.2. If from the first point the grade average goes up by .1 point per additional hour of study, on the average, then what time of study corresponds to the second point?
12. You graduate from college and start a job at a salary of $40,000 / year. You get regular raises and at the end of 10 years you are making $60,000 / year. What is your best estimate of how much money you make during the 10-year period?
13. Coasting down a hill your speed at one point is 20 feet / second and your speed at another point is 30 feet / second. If it takes 8 seconds to get from one point to the other then what is your best estimate of the distance between the points?
14. Water enters a container at an increasing rate. At a certain instant t0 the rate is 10 gallons/minute. At a certain later time the amount of water that has flowed into the container starting from the instant t0 is 75 gallons, and water is flowing at a rate of 20 gallons / minute. What is your best estimate of the time required for the 75 gallons to flow into the container?
15. On a graph of rate R vs. clock time t, where R is the rate at which you earn money in dollars / month and t is measured in months, sketch the points corresponding toa rate of $2000 / month at t = 5 months and a rate of $3000 / month at t = 15 months. Sketch a line segment connecting the points.
· Use your graph to find the average rate at which you are earning money during this 10-month span.
· How much money do you earn during this period?
· How can this quantity be found from your graph?
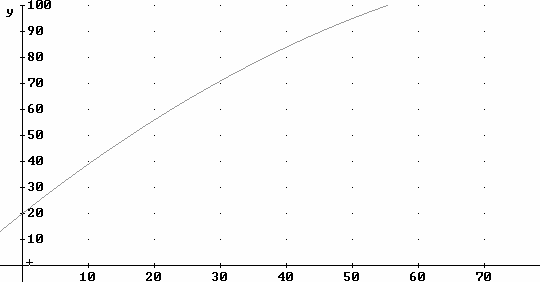
16. The graph below represents the speed v of an object, in meters / second, vs. clock time t, measured in seconds. Use your graph to answer the following questions. How fast is the object moving at t = 5 seconds? How fast is it moving at t = 10 seconds? What is its average speed over this 5-second interval? How far does it travel during this interval?
1. Suppose that the depths of water in a uniform cylinder at clock times t = 0, 10, 20, 30, 40 and 50 seconds are respectively y = depth = 100, 80, 64, 52, 44 and 40 cm.
· By how much does depth change during each 10-second interval?
· Do these changes form a predictable sequence?
· For each interval at what average rate does depth change with respect to clock time?
2. Sketch the depth vs. clock time data points of the preceding problem. Connect each point with the next by a straight line segment. Using this graph estimate the depths at t = 5 seconds and at t = 45 seconds. Do you think your estimates of the actual depths of the water are high or low, and why?
3. Sketch the depth vs. clock time data points of the preceding two problems. Sketch a smooth curve passing through your data points. If you were to use your curve to estimate the depths at t = 5 second and at t = 45 seconds do you think your results will be higher or lower than those you obtained from the preceding graph? Why is this? What are your estimates?
1. You have a large box full of tiles, each 1 foot square. Describe how you would cover a rectangle whose dimensions are 3 ft by 5 ft using tiles from this box. {}Describe how you would cover a square 2 feet on a side. How many tiles would be required?{}Describe how you would cover a square 3 feet on a side. How many tiles would be required?{}Describe how you would cover a square 4 feet on a side. How many tiles would be required?{}Describe how you would cover a square 20 feet on a side. How many tiles would be required?{}{}If you graph the number of tiles required to cover a square vs. the length of a side of the square what does your graph look like?
2. You have a large box full of tiles, each 1 inch square. Describe how you would cover a rectangle whose dimensions are 4 in by 7 in using tiles from this box. How many tiles would be required if the dimensions of the rectangle doubled?
3. You have a large box full of cubical blocks, each 1 foot square. Describe how you would fill a cube 3 feet on a side with blocks, so that the entire cube was completely filled. How many cubes would be required?{}Describe how you would fill a cube 4 feet on a side with blocks, so that the entire cube was completely filled. How many cubes would be required?{}Describe how you would fill a cube 2 feet on a side with blocks, so that the entire cube was completely filled. How many cubes would be required?{}Describe how you would fill a cube 10 feet on a side with blocks, so that the entire cube was completely filled. How many cubes would be required?{}{}If you graph the number of tiles required to fill a cube vs. the length of a side of the cube what does your graph look like?
4. You have a large box full of cubical blocks, each 1 inch square. Describe how you would fill a rectangular solid with blocks, so that the entire cube solid was completely filled, if the base of the solid is a rectangle whose dimensions are 5 inches by 4 inches and whose uniform altitude is 3 inches. How many cubes would be required?{}Describe how you would fill a rectangular solid whose dimensions are double those of the solid given in the preceding. How many blocks would be required?{}How does the number of blocks required to fill a solid change if the dimensions of the solid are doubled?
5. What is the area of the base of the solid of the preceding problem? What is its altitude? How can the area of the base and the altitude be combined to obtain the volume? In terms of the 1-inch cubes, why does it make sense that this is the case?
6. What is the length of the diagonal of a rectangle whose length and width are respectively 9 and 5?
7. You can't cover a square 1.5 feet on a side with uncut 1-foot-square tiles. However you can cover a square with double these dimensions with 1-foot-square tiles. How many 1.5-foot squares would be required to cover the doubled square? How many 1-foot-square tiles would be required to cover this doubled square? How can you use this to conclude the area of the 1.5-foot square?
8. How many squares each 1.25 feet on a side would be required to make a square which can be covered with uncut 1-foot-square tiles? How many 1-foot-square tiles would be required to cover this larger square? How does this result allow us to find the area of the 1.25-foot square?
9. If the length of an edge of a square is 81/17 feet, then how many of these squares would be need in order to build a square which can be covered with 1-foot-square tiles? How many 1-foot-square tiles would be required to cover this square? How does this result allow us to find the area of the 81/17-foot square?
10. You can't precisely fill a cube 1.5 feet on a side with uncut 1-foot cubical blocks. How many 1.5-foot cubes would it take to build a cube which could be filled with uncut 1-foot cubes? How many 1-foot cubes would it take to fill this larger cube? How can you use these results to find the volume of the 1.5-foot cube?
11. How many 2.2-foot cubes would it take to build a cube which could be filled with uncut 1-foot cubes? How many 1-foot cubes would it take to fill this larger cube? How can you use these results to find the volume of the 2.2-foot cube?
12. How many cubes with edge length 15/29 would it take to build a cube which could be filled with uncut 1-foot cubes? How many 1-foot cubes would it take to fill this larger cube? How can you use these results to find the volume of the 15/29-foot cube?
13. A rectangle has length 20/3 and width 5/8. How many such rectangles would we have to put together to form a rectangle which can be covered by uncut 1-foot squares tiles? How many 1-foot tiles would be required to do this? How can you use these results to find the area of the 30/3 x 5/8 rectangle?
14. A rectangle has length 7/6 and width 5/8. What is the minimum number of such rectangles we would have to put together to form a rectangle which can be covered by uncut 1-foot squares tiles? How many 1-foot tiles would be required to do this? How can you use these results to find the area of the 30/3 x 5/8 rectangle?
15. If the diagonal of a rectangle is 8 and its width is 5 then what is its length?
16. If the diagonal of a square is 7 then what are the lengths of its edges?
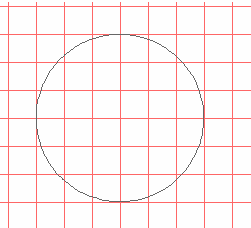
17. The figure below shows a circle of radius 3 ft on a grid of 1-foot squares. How many 1-foot squares lie entirely inside the circle? What is the total area of these squares? Estimate how much area is left inside the circle but outside the squares you counted.
18. The figure below shows a circle of radius 3 ft on a grid of 1/2-foot squares. How many 1/2-foot squares lie entirely inside the circle? What is the total area of these squares? Estimate how much area is left inside the circle but outside the squares you counted.
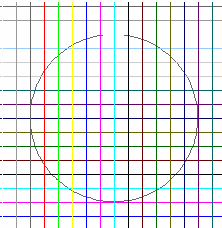
18. The figure below shows a circle of radius 3 ft on a grid of 1/4-foot squares. How many 1/2-foot squares lie entirely inside the circle? What is the total area of these squares? Estimate how much area is left inside the circle but outside the squares you counted.

19. The figure below shows a circle of radius 3 ft on a grid of 1/8-foot squares. How many 1/2-foot squares lie entirely inside the circle? What is the total area of these squares? Estimate how much area is left inside the circle but outside the squares you counted.
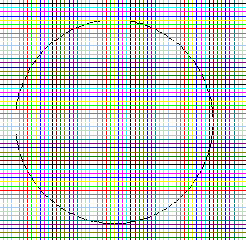
20. Write your areas inside the squares from the preceding four questions as a sequence. Do the numbers in your sequence change by greater and greater amounts or by lesser and lesser amounts? This process could be continued indefinitely, though you would quickly get tired of counting. The 4-number sequence you wrote down is therefore the beginning of an infinite sequence. Is there a limit to how large the numbers in this infinite sequence can get?
21. Write your 'leftover' areas as a sequence. Do the numbers in your sequence change by greater and greater amounts or by lesser and lesser amounts? As before this sequence is the beginning of an infinite sequence. Is there a limit to the values of the numbers in this sequence?
22. The figure below is a top view of a cylinder of radius 3 ft and altitude 5 ft. The grid depicts a top view of an array of 1-foot cubes. The second figure is a side view of the cylinder and the array of cubes. How many 1-foot cubes are contained completely inside the cylinder? What is the total volume of these cubes? Estimate how much volume is left inside the cylinder but outside the cubes you counted.
23. The figure below is a top view of a cylinder of radius 3 ft and altitude 5 ft. The grid depicts a top view of an array of 1/2-foot cubes. The second figure is a side view of the cylinder and the array of cubes. How many 1/2-foot cubes are contained completely inside the cylinder? What is the total volume of these cubes? Estimate how much volume is left inside the cylinder but outside the cubes you counted.
24. The figure below is a top view of a cylinder of radius 3 ft and altitude 5 ft. The grid depicts a top view of an array of 1/4-foot cubes. The second figure is a side view of the cylinder and the array of cubes. How many 1/4-foot cubes are contained completely inside the cylinder? What is the total volume of these cubes? Estimate how much volume is left inside the cylinder but outside the cubes you counted.
25. The area of a circle is, as you probably know, given by the formula A = pi r^2. What is the area of the circle of the preceding set of problems? Does the sequence of areas written in response to the first few questions appear that it might approach this area as a limit? Justify your answer.
26. What do you think is the precise volume of the preceding cylinder? Reason this out in terms of what you have seen so far in this course; don't use a formula given in a textbook. Think it through and justify your answer.
27. What would be the volume of a cylinder whose diameter is 2 cm and whose altitude is .3 cm? Would this cylinder be closer in size and shape to a CD, a 50-gallon barrel, a quarter or a quarterhorse?
28. A circular hoop of radius 3 feet is balanced on the ground so that the circle is vertical. Sketch this circle and sketch the vertical diameter of the circle. {}{}Form a triangle as follows: Start from the center and move up the vertical diameter until you are 5 feet off the ground. Then move in the horizontal direction until you meet the circle. Then move on a straight line back to the center of the circle. What are the lengths of the sides of your triangle?