Precalculus I Class Notes: Function Families

Precalculus I Class Notes 9/08/98

Introduction to Function Families

Analyzing a Quadratic Function

We analyze a quadratic function y = a t^2 + b t + c by determining the locations of its zeros, if any, the location of its vertex, the points 1 unit to the right and left of the vertex, and the y intercept. We can find the value of y corresponding to a given value of t by substitution; we can fine the value(s) of t corresponding to a given y using the quadratic formula.

Basic Function Families

The first three of the four basic functions are y = x, y = x^2 and y = 2^x. We graph these functions by first making a table for each. We see that y = x yields a straight-line or linear graph, y = x^2 yields a parabolic graph with vertex at the origin, and y = 2^x yields a graph which is asymptotic to the negative x axis and which increases more and more rapidly for increasing values of x.

Stretching and Shifting the Basic Functions

When a graph is stretched vertically by a given factor a, every point on the graph moves in the vertical direction until it is a time as far from the horizontal axis as it was before. If | a | is less than 1, every point moves closer to the horizontal axis and the graph appears to be compressed; if | a | is greater than 1, every point moves further from the horizontal axis and the graph appears stretched. If a < 0, then positive values of the basic function are transformed into negative values and negative values into positive, and the graph appears inverted. When the linear function y = x is vertically stretched by factor a the its slope is multiplied by a.

When a graph is shifted either horizontally or vertically, every point moves the corresponding horizontal or vertical distance, and the graph simply shifts left or right, or up or down, as the case may be.

When applying a series of stretches and shifts to a graph, we always apply the stretches first. Applying the shifts first would give a different result.

A variety of function families can be generated by applying one or more fixed transformations, and by also applying a transformation whose parameter varies over a given range.

The Number of Transformations Required to obtain the General Function for each Basic Function

A linear function is characterized by its slope and y intercept. It requires only a vertical stretch of the basic y = x function to match the slope of any desired linear function, and only a vertical shift to match the y intercept.

A quadratic function y = a t^2 + b t + c is characterized by the location of its vertex and by the value of a. It requires only three transformations to transform y = t^2 into a given quadratic. We first stretched the function vertically by factor a, then shift it horizontally and vertically to reposition the vertex.

A general exponential function y = A * 2^(kt) + c can be obtained from y = 2^t by a vertical stretch by factor A, a horizontal stretch by factor 1/k (or the horizontal compression by factor k), and a vertical shift c.

Analyzing a Quadratic Function

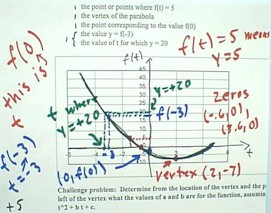
Given the graph of a quadratic function, as shown below, we wish to indicate

the zeros of the function

the point or points where f(t) = 0

the vertex of the parabola

the point corresponding to the value f(0)

the value y = f(-3)

the value of t for which y = 20.

The zeros are the points where the graph crosses the t axis.

We estimate these points to be (-.6, 0) and (4.6, 0) [note: not (3.6, 0) as incorrectly labeled in the figure).

The expression f(t) = 5 means that f(t), whose value is plotted on the vertical axis, has the value 5.

Thus we look for the point on the graph where the vertical coordinate is 5.
This point is approximately -1.5, 5; its projection lines to the horizontal vertical axes are indicated in red.

The vertex of the parabola is the extreme point of the parabola and lies on the axis of symmetry.

We estimate this point to be approximately (2, -7).

When we refer to f(0), we are talking about the value of f(t) when t = 0.

We therefore look for the graph point corresponding to t = 0.
Since t = 0 on the vertical axis, we see that we are looking for the point at which the graph crosses the vertical axis.
This point is approximately (0, -3), and is indicated as (0,f(0)) on the graph.

In the expression y = f(-3), we see that the -3 replaces t in the expression y = f(t).

We thus look for the graph point corresponding to t = -3.
This point is found by following the blue dotted line up from the t axis to the graph; the line continues over to the vertical axis, where we label the value f(-3). This value is a bit less than 20.

To find the t value of the function for which y = 20, we locate the y = 20 point on the vertical axis and proceed straight across to the graph to the y = 20 point.

We then project straight down to the t axis to find the t value, which is a bit less than -3.

video clip #01

http://youtu.be/5h1HwFLQgKc

If we wish to find the values of a, b and c for the quadratic function y = a t^2 + b t + c, we note that the graph gives us the following information:

The vertex is at x = 2, so -b / (2a) = -2.
If we go over one unit from the vertex we go up about one unit (it's a bit hard to tell for sure be to the scale of the graph, but 1 vertical unit seems about right). So we figure that a = 1.
Since a = 1 and -b / (2a) = -2, we must have -b / (2 * 1) = -2, so b = -4.
Since for t = 0, y = f(t) = a t^2 + b t + c takes value f(0) = c, c = -3 (again estimating the y coordinate corresponding to t = 0 from the graph).

Our function is thus approximately y = 1 t^2 - 4 t - 3.

Basic Function Families

Before introducing the idea of basic function families, we review of couple of essential facts about exponents.

In the first place, b^x * b ^ y = b ^ (x + y).

This isn't a rule made up to confuse algebra students, but is simple common sense about multiplying numbers:

b^x means b multiplied by itself x times, and b^y means b multiplied by itself y times.

So b^x * b^y will consist of b multiplied by itself a total of x + y times. Again, just common sense.

It follows from this that, for example, 2 ^ -2 * 2 ^ 2 = 2 ^ (-2 + 2) = 2 ^ 0.

People often make a mistake of thinking that 2 ^ 0 = 0, but this seemingly commonsense assumption actually violates common sense.

This can easily be seen as follows:

2 ^ -2 = 1 / (2^2) = 1/4 (recall that raising a number to a negative exponent results in an inversion of sort e.g., 2 ^ -2 = 1 / (2^2) = 1/4).

So when we multiply 2 ^ -2 by 2 ^ 2 we get 1/4 * 4 = 1.

It follows that 2 ^ 0 = 1.

We could duplicate this argument for any number b, coming to the conclusion that b ^ 0 = 1 for any number b.

video clip #02

http://youtu.be/Xlhdi9i7rT8

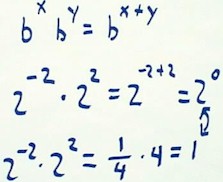
We now introduce the first three of our four most basic function families.

These are the families of the functions

y = x,

y = x^2 and

y = 2 ^ x.

We begin by making a table for each of the functions, using x values from -3 to 3.
We observe the different behaviors of the four functions. We note:

the constant changes in y values for the y = x function,

the symmetry of the y = equal x ^ 2 function, and

the fact that the y = 2^x function doubles with every successive x value on the table.

video clip #03

http://youtu.be/da16stlP4k8

We sketch the graphs of these functions.

Not surprisingly the y = x function has a graph which is a straight line through the origin.
The y = x ^ 2 function has a graph in the shape of a parabola, symmetric about the y axis.
The y = 2 ^ x function approaches the negative x axis more and more closely as x becomes more and more negative, while the graph gets steeper and steeper for increasing positive values of x.

The y = 2 ^ x function is called an exponential function; exponential functions all have the same basic shape, though some might be upside down and some inverted from left to right as compared to the function shown here.

On one side or another an exponential function always approaches a horizontal line, coming closer and closer without limit but never quite reaching the line.

This line is called a horizontal asymptote of the graph.

video clip #04

http://youtu.be/Fi46zzNiRfk

Stretching and Shifting the Basic Functions

Starting with a basic function, we can think of stretching its graph either in the vertical or the horizontal direction, or both, then shifting the graph to the right or left (horizontally) or up or down (vertically).

As we will see, such transformations leave straight lines straight, leave parabolas parabolas, and transform graphs of exponential functions into graphs of other exponential functions.

If we consider what happens to a parabola when we stretch it vertically, we will gain valuable insight into how this process works.

Begin with the basic parabola y = x ^ 2. This graph is shown in blue in the figure below.
To stretch the graph vertically by a factor of 2, we take each point of the original (blue) graph and move it twice as far from the x axis to obtain the red graph.
This has the effect of doubling the value of y that corresponds to each value of x.
As a result the function y = x^2 is transformed into the 'doubled' function y = 2 x ^ 2.

We could also have stretched the y = x ^ 2 graph by a factor of 1/2, moving each point of the y = x ^ 2 graph to 1/2 its distance from the x axis.

Since each y value is halved, we see that the new function is y = 1/2 x^2.

We can even extend the idea of stretching to negative factors.

If we stretch the function y = x ^ 2 by factor of -1, we will maintain the distance of every point from the x axis but will reverse its direction from the x axis.
This says the effect of inverting the graph, as shown below.

video clip #05

http://youtu.be/m5rV1nf7e9U

If we apply the same stretching idea to a linear graph, we see that stretching by a factor of 2, as it moves every point twice as far away from the x axis, has the effect of doubling the slope of the graph.

Suppose we wish to match the green dotted line (supposed to be straight but not quite looking that way), using just stretching and shifting transformations. How would we go about it?

video clip #06

http://youtu.be/ENAVd7ud_Ec

If we wish to match the green dotted line using just stretching and shifting transformations, we might begin by applying a stretching transformation.

Note that we always apply stretching transformations before shifting transformations.

We begin by stretching the graph by a factor of approximately 1/3 (this is just an estimate based on the graph; 1/4 might also be close for this graph).
This gives us the graph of the function y = 1/3 x.

Then to match the green graph, we would have to raise the graph an estimated 6 units.

This is indicated by the purple vertical arrows 'lifting' selected points of the 'red' graph to the target 'green' graph.
This process increases the values of y = 1/3 x by 6, resulting in the graph of the function y = 1/3 x + 6.
We note that this shift raises the point (0,0) to (0,6). The latter point is called the y-intercept of the graph of y = 1/3 x + 6.

More generally, if we stretch the y = x graph by factor m, then raise it b units vertically, we obtain the graph of the general linear function y = mx + b.

The factor m is the 'vertical stretch' factor and gives us the slope of the graph of the transformed function.
The vertical shift b raises the origin to (0,b), which is called the y intercept of the graph.
Thus the function y = mx + b has a graph whose slope is m and its y intercept is at (0,b).

We can see the variety of graphs possible for this general linear function by imagining that the parameter b is held fixed, which results in a fixed y intercept, while the parameter m is permitted to vary through all possible real numbers.

The first figure below gives representative members of this family.

We might on the other hand wish to keep m constant and let b vary.

This would result in a series of graphs with the same slope, and hence parallel to one another, though with different y intercepts.
Representatives of this family are sketched in the second graph below.

video clip #07

http://youtu.be/Df7h5dx92wc

The Number of Transformations Required to obtain the General Function for each Basic Function

Any linear function can be constructed by two geometric transformations: a vertical stretch and a vertical shift.

These two transformations are related in the way discussed above to the two parameters m and b in the general form y = mx + b of a linear function.

Each independent transformation we apply to a function will be related to a parameter in the general form of the function.

To obtain a given parabola by geometric transformations we must usually employ three transformations, a vertical stretch to get the 'width' of the parabola correct, then a horizontal and a vertical shift.

We know that a parabolic (or quadratic) function has the general form y = a x^2 + b x + c, with three parameters.
These parameters are determined by the transformations, but each transformation is not directly related to exactly one of the parameters (as we will see, one of the transformations directly determines the value of a, but the other two have a combined influence on b and c).

Another way of expressing the basic form of a quadratic function is y = a (x - h) ^ 2 + k.

This form is completely equivalent of the other, but a is the vertical stretch, the h is the horizontal and k is the vertical shift.

When we stretch and shift our basic exponential function y = 2 ^ x, we will think of a vertical stretch, a horizontal compression, and a vertical shift.

Again we use three geometric transformations and we obtain a function form with three parameters.
One form is y = A b ^ x + c, with parameters A, b and c; another is y = A * 2 ^ (kx) + c, with parameters A, k and c.

The second of these forms reveals the vertical stretch A, the horizontal compression k and the vertical shift c.

Just as a we were able to fit a quadratic function to any three data points, we can fit an exponential function to any three data points.

We substitute the coordinates of the three points into one of the forms above, or a third equivalent form to be discussed later, and obtain three simultaneous equations.
The equations we got for the parameters of the quadratic model were linear so we could solve them by adding multiples of equations to one another and multiplying equations by constants; the equations we get for the exponential model are not linear and must be solved by other means. But the principal is the same in that we obtain three simultaneous equations and solve them for the parameters of the model.

video clip #08

http://youtu.be/ZalNjnaogKE