"
Class Notes Precalculus I, 9/22/98
Symbolic Slopes; Slope = Slope Equation
We can find a straight line which we have fit to a set of data by choosing two points
on the line and plugging their coordinates into the form y = mx + b of a linear function.
We wish to fit a straight line to
the spring length vs. load data plotted on the graph below, and to determine the linear
function for that line.
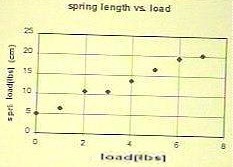
We begin by sketching a line which seems to fit the points as well as possible. The
sketch below is a reasonable attempt at such a line, though it could be improved upon.
- Having sketched the line we select a pair of points, not too close together, from which
to determine the equation of the line.
Here we choose points (2,8) and (8,23).
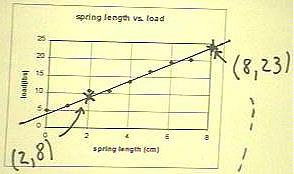
We then substitute the coordinates of the points into the general form y = mx + b of a
linear function.
- We obtain two equations in the
unknowns m and b.
- Subtracting the two equations we
eliminate b and obtain 15 = 6 m, which we solve for m.
- We obtain m = 2.5 (note the error
in the figure: x = 2.5 should read m = 2.5).
- This value is substituted back
into the second of the original equations to obtain an equation for b, which we solve.
- We substitute the values we have
obtained for m and b into the y = mx + b form to obtain the equation y = 2.5 x + 3.
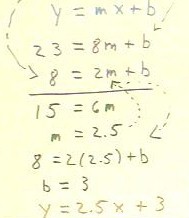
Video Clip #01
http://youtu.be/H9biVygTnhE
At this point we can if we wish note that y stands for spring length and x for load,
and rewrite the equation as
springLength = 2.5 * load + 3.
This form does not require us to remember what x and y stand for as we pose and answer
questions regarding model.
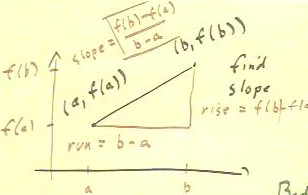
The next problem posed was to find the slope of the line between the points (a, f(a))
and (b, f(b)) on the graph of some unspecified function y = f(x).
- We begin by constructing the slope triangle and, to keep the symbolic quantities
straight, labeling the positions a and b on the x axis and the corresponding positions
f(a) and f(b) on the y axis.
- It is then clear that the run from the first point to the second is b - a, and that the
rise is f(b) - f(a).
- We can thus write our desired result:
- slope = rise / run = (f(b) - f(a)) / (b-a).
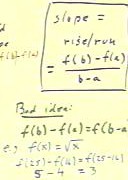
When this problem was done in class several individuals had the good idea to simplify
the expression.
- This is in fact something that we would wish to do if it was possible.
However the expression does not simplify, at least not without further information about
the function f(x).
Well-intentioned attempts to simplify revealed two bad ideas, discussed below.
The first bad idea, illustrated in the lower right-hand corner of the figure below, is
to treat the expression f(b) - f(a) as if f(x) indicated multiplication of x by f, rather
than the functional relationship it in fact indicates.
- Looked at in this way it certainly looks like the distributive law applies so that f
factors out and f(b) - f(a) = f(b-a).
However, this is not correct.
- That this is not the case is easily illustrated by specifying almost any nonlinear
function f(x) and choosing almost any two numbers for a and b.
- For example in the figure we choose f(x) = `sqrt(x), a = 25 and b = 16.
Then if f(b) - f(a) = f(b-a), we would have f(25) - f(16) = f(25 - 16).
For for this function we would thus have `sqrt(25) - `sqrt(16) = `sqrt(25-16).
This simplifies to the statement 5 - 4 = 3.
Since this is clearly false we see the error in assuming the distributive property for
function notation.
Note that in the video clip it is stated that f(b) - f(a) = f(b-a) holds true for
linear functions.
- This statement is false, and
clearly illustrates that your instructor too can unthinkingly fall prey to bad ideas.
- You might pick a linear function
whose y intercept is not 0 and test the instructor's statement to see why this is false.
- The statement what have been true
if the instructor had restricted the statement to linear functions with y-intercept 0; you
might check this out.

Video Clip #02
http://youtu.be/DUeqBtp7ahY
A second bad idea, much worse than the first (with all due respect to its originator,
who usually has good ideas), is illustrated in the lower left quadrant of the figure above.
- This is the idea that (f(b) - f(a)) / (b-a) = f(b) / b - f(a) / a.
We can substitute just about any numbers for a, b, f(b) and f(a) and see that this
statement is false.
There is in fact nothing at all in the properties of real numbers that justifies such a
step.
The first bad idea at least looked like the distributive law, this one looks like really
bad order of operations, which is why this idea is worse than the former.
We now look at another method of finding the equation of the straight line through two
given points.
- In the figure below we begin with the points (1,4) and (8,9).
We will make use of a simple but profound picture and the fact that the slope between
any two points lying on a straight line is the same.
The equation of a straight line y = mx + b is in fact the test of whether the point (x,y) lies on the line.
- If the point lies on the line then the equations satisfied.
Otherwise the equation is not satisfied.
To construct the straight line, we first sketch the slope triangle between the two
points and determine the slope, which in this case is clearly 5/7.
- Since the slope of a straight line is constant, this will be the slope between any two
points on the line.
We next place a point (x, y) at an arbitrary position on the line.
- We construct the slope triangle between (x, y) and one of the two given points.
In the figure below we select the first point, and construct a slope triangle whose run
is x - 1 and whose rise is y - 4.
The slope between (1,4) and (x, y) is thus seen to be (y-4) / (x-1).
As mentioned before, we use the fact that the slope between any two points on the
straight line must be the same.
- We can therefore say that if the point (x, y) lies on the line, then the two slopes we
have just obtained must be equal. We can therefore write
This relationship will be satisfied by the point (x, y) if, and only if, that point lies on the straight line
through the two given points.
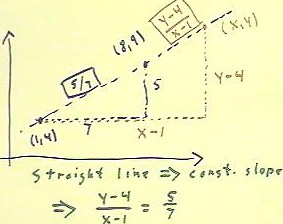
Since this equation was obtained by setting two slopes equal to each other, we call
this the 'slope = slope' form of the equation of a straight line.
- We can put this equation into the
standard y = mx + b form of the equation of a straight line by simply solving it for y.
We begin with the equation and we carefully use valid algebraic laws to arrive at our
solution.
- To isolate y, we first multiply both sides by the denominator (x-1) of the left-hand
side.
We then note that (x-1) / (x-1) = 1, so that (y-4) / (x-1) * (x-1) = y-4, obtaining the
third equation below.
At this point we have a choice of adding 4 to both sides, which will accomplish our goal
of isolating y, or first applying the distributive law to the right-hand side.
Either choice is good. Someone suggested applying the distributive law first, so we
follow this suggestion.
- After applying the distributive law in a straightforward fashion, we proceed to add 4 to
both sides, finally isolating y. (Note that -5/7 + 4 = -5/7 + 28/7 = 23 / 7).
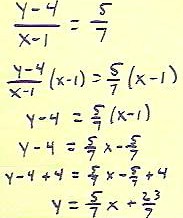
Video Clip #03
http://youtu.be/xymarqZHAxY
More than one student commented
in class that it is easier to solve this problem if we convert everything to decimals.
- It is true that in some senses decimals are easier to work with then fractions, and this
is especially true for students who have grown up doing all their mathematics on a
calculator and who have never really learned to work with fractions.
However, in many applications small errors have a way of amplifying themselves into
serious errors.
The fractions involved in this problem, and most fractions that we encounter in
applications, are expressed by calculators in decimal forms that have a slight round-off
error.
For this and other reasons it is important to be able to solve problems involving
fractions.
The process is somewhat tedious but not particularly difficult, and it also illustrates
the use of the common-sense rules of algebra.
One individual had the very good idea of getting rid of all the denominators in this
problem. This is a standard procedure and a great idea; it 'clears' all the
fractions and leaves us with whole numbers up to the very last step.
- Having arrived at the third step, where y - 4 = 5 / 7 * ( x - 1), this individual
proceeded to multiply both sides of the equation by 7, correctly obtaining the indicated
expression.
However in the next step the right-hand side became 35 x - 35.
When multiplying the expression in parentheses by 7, the individual forgot about the 7
in the denominator, which divides the 7 out front.
So we see a very good idea and a bad idea expressed in one solution.
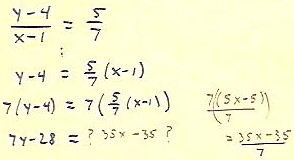
Video Clip #04
http://youtu.be/XVWq1ISS_KI
We now generalize the process of finding the equation of a line through to
given points.
- If the points are given by the symbolic expressions (x1, y1) and (x2, y2), we can easily
follow the same process we used before with numerically specified points.
We begin by finding the slope between the two points.
- Clearly the run is x2 - x1 and the rise is y2 - y1, so the slope is (y2 - y1) / (x2 -
x1).
If we locate an arbitrary point (x, y) on the line and construct its slope triangle with
the point (x1, y1), we obtained a rise of y - y1 and a run of x - x1, and therefore a
slope of (y - y1) / (x - x1).
Setting the two slopes equal we have the slope = slope equation
- (y - y1) / (x - x1) = (y2 - y1) / (x2 - x1).
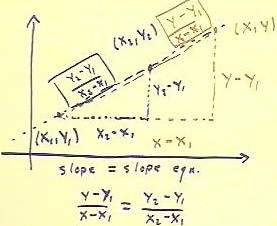
This slope = slope equation is easily rearranged, by multiplying both sides by x - x1,
into the perhaps familiar but possibly forgotten 'point-point form' of the equation of the
straight line.
- At some point in your mathematical career you have been asked to memorize this equation.
The approach of this course is to begin with the simple picture we have used to develop
the slope = slope equation and to proceed logically to obtain that equation.
The ability to know where to start and to move logically from premises to conclusion is
far more important then the ability to memorize and apply a meaningless equation.
It is possible to associate a picture with the point-point form, but the picture is not
as simple and elegant as the picture that goes with the slope = slope equation.
You are therefore expected to be able to sketch the picture and proceed
logically to the slope = slope equation.
We note that if the slope is already known, it can then be substituted for (y2 - y1) /
(x2 - x1).
- This is of course particularly valuable if we don't happen to know two points.
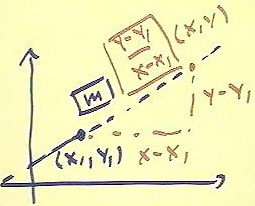
If we know a single point (x1, y1) and the slope m then the slope = slope equation
becomes (y - y1) / (x - x1) = m.
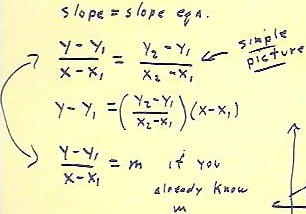
The situation corresponding to knowing a single point and the slope is illustrated
below.
- We construct a single slope triangle between the known point (x1, y1) and the arbitrary
point (x, y) on the line.
We set the slope of this triangle equal to the known slope m, obtaining as before (y -
y1) / (x - x1) = m.
Video Clip #05
http://youtu.be/DNmw431a6sI
"
