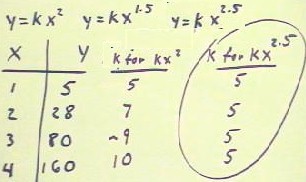Proportionality

Class Notes Precalculus I, 10/06/98

Proportionality

The quiz problem was to determine whether the y vs. x data in the figure below is most appropriately fit by which of the following proportionalities:

y = k x^2,
y = k x^1.5 or
y = k x^2.5.

We can test whether the y = kx^2 proportionality is appropriate by evaluating k for different data points.

The data point (1, 5) gives us 5 = k (1^2), which we solve to obtain k = 5.
Using the same procedure for the remaining three data points we obtain k values 7, approximately 9, and 10.
Since these values are all different, and since they follow a clear pattern of increasing, we will not regard y = kx^2 as a particularly good model.

If we repeat this procedure for y = k x^2.5, we find that all k values turn out to be very close to 5.

This indicates that y = 5 x^2.5 is a good candidate for our model.

Had we used y = k x^1.5, we would have had results similar to those for y = k x^2, except that the k values would have increased even more, from 5 to 20 for the given data.

Video File #01

http://youtu.be/AWd8zqPZfMc

Randomized Proportionality Problems, Version 1

The first problem asks by what factor the volume of a cube changes when the length of its side increases from 7 to 8.

We could of course answer this by simply finding the volume of each cube.
We would find volumes 343 and 512, so volume changes by factor of 512 / 343.

However, we prefer to use proportionality to answer this question.

Proportionality will give us the correct result for a similar problem posed with regard to the volumes and diameters of a pair of spheres, the volumes and altitudes of a pair of geometrically similar cones, the volumes and main diagonals of a pair of geometrically similar rectangular solids, or more generally comparisons involving the volume and any linear measure (a linear measure is anything can be measured with a tape measure or a piece of string) of two geometrically similar solids.

We begin with our knowledge that the volume of a cube is proportional to the cube of its side (more generally, we would use the knowledge that the volume of a given shape is proportional to the cube of any linear dimension, e.g., the volume of the sphere is proportional to the cube of its diameter).

We write V = k x^3.

Now if we have to side lengths x1 and x2, we will have volumes V1 = k x1^3 and V2 = k x2^3.

We will proceed to find an expression for the ratio of these volumes.

We easily obtain the ratio of these volumes, as shown below.

Note that (k x2^3) / (k x1^3) = (k/k) * (x2^3 / x1^3) = x2^3 / x1^3, and x2^3 / x1^3 = (x2 / x1) ^ 3.

For the present problem we see that (V2 / V1) = (8/7) ^ 3 = 512 / 343 = 1.5 (approx) as shown in the upper right-hand corner of the figure below.

We thus see that an increase from side length 7 to side length 8, an increase of approximately 14% in the side length, results in an increase of about 50% in the volume.

We note that V2 / V1 is indeed the factor by which the volume changes.

For example if V2 / V1 was 2, we would certainly say that the volume doubles.
This is the same as saying that the volume changes by a factor of 2.

Video File #02

http://youtu.be/LOlcOPkMehE

The second problem asks for the factor by which the area of a square will change if its diagonal increases from 8 to 9.

We note that diagonal is a linear measure -- it could easily be measured with a tape measure.
As such it is proportional to side length (d2 / d1 = s2 / s1)
The area is therefore proportional to the square of diameter.
Thus we can say that area is proportional to the square of the diameter: A = k d^2.

Proceeding as we did on the first problem, we find the ratio of A2 = k d2^2 to A1 = k d1^2.

The algebra is practically identical to that used before; the only difference is that the power is now 2 instead of 3.
We therefore see fairly quickly that A2 / A1 = (d2 / d1) ^ 2.
Therefore a change from diameter 8 to diameter 9 will result in an area change by factor A2 / A1 = (9/8) ^ 2 = 1.27 (approx.).

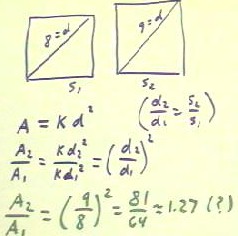
Video File #04

http://youtu.be/x6GuQNdiVuc

The next problem requests the factor by which the side length changes when the volume of the cube changes from 85 to 8.

In this problem we want to write the proportionality of side length to volume, not volume to side length as we have done before.

Knowing that the volume is proportional to the cube of the side length, V = k x^3, we can easily solve for side length x.

We multiply both sides of the equation by 1/k, obtaining V / k = x^3.
We then take the 1/3 power of both sides of the equation, obtaining x = (V / k) ^ (1/3).
Noting that (V / k) ^ (1/3) = (1/k) ^ (1/3) * V^(1/3), we express the constant number (1/k) as H (using a pretty fancy-looking, if poorly constructed, H).
Since k is constant, H = (1/k) is also constant and we can write x = H V^(1/3).

We can now follow the same procedure used before, obtaining the result (x2 / x1) = (V2 / V1) ^ (1/3).

The figure below shows what we get when we substitute V2 = 8 and V1 = 85.

We express the proportionality in this problem by saying that since volume is proportional to the cube of the side length, side length must be proportional to the cube root, which is the 1/3 power, of the volume.

The algebraic steps we have followed justify this type of reasoning and, once we are secure with the algebraic steps, we can confidently skip them in simply write x2 / x1 = (V2 / V1) ^ (1/3).

Video File #05

http://youtu.be/BwuIN9v-aRk

The next problem employs this kind of reasoning.

Given that the area of a square changes from 69 to 2, we wish to find the factor by which side length changes.
Since area is proportional to the square of the side, we conclude that the side must be proportional to the square root, or the 1/2 power, of the area.
We therefore write x = k A^(1/2), from which it follows by the usual steps that (x2 / x1) = (A2 / A1) ^ (1/2).
Using the given areas, we therefore find that x2 / x1 = (2/69)^(1/2).

Video File #06

http://youtu.be/03vmynk83xc

The next problem introduces a somewhat more complicated type of reasoning.

We are given the volumes of two cubes and asked for the factor by which their areas change.

We know that volume is proportional to the cube of side length, and that area is proportional to the square of side length.
But what is the proportionality between area and volume?
That is, what power p do we use for the proportionality A = k V ^ p?

Our strategy will be to write down what we know and see what we can do with it.

We write down the proportionalities A = k_A x^2 and V = k_B x^3, where k_A is the proportionality constant for area and k_V is the proportionality constant for volume.
We then note that we don't care much about side length x, which doesn't appear in the statement of the problem.
This suggests that we might eliminate x from these two proportionalities to obtain the relationship between A and V.

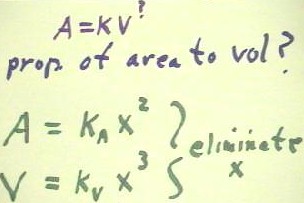
Solving for x, we obtain x = (V / k_V) ^ (1/3).

Substituting this into the expression for A we obtain A = k_A ( (V / k_V)^(1/3) ) ^ 2.
By the laws of exponents this gives us

A = k_A ( V / k_V ) ^ (2/3).

This could be rearranged to the form A = k_A / (k_V) ^ (2/3) * V^(2/3).
Then if we let k = k_A / (k_V) ^ (2/3), we can write A = k V^(2/3).

This justifies the following sort of proportionality reasoning:

If area is proportional to the square of side length, and volume is proportional to the cube of side length, then side length is proportional to the cube root of volume.
Since area is proportional to the square side length, then area is proportional to the square of the cube root of volume, which is the 2/3 power of volume.

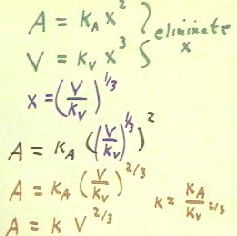
Having obtained the proportionality A = k V^(2/3), we easily see that A2 / A1 = (V2 / V1) ^ (2/3), and use this to determine area ratio when the volume changes from 52 to 8.

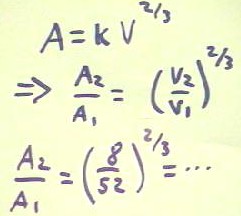
Video File #07

http://youtu.be/0r7Id_OQulk

The figure below shows the reasoning we would use to find the ratio of periods T given information about pendulum length L, knowing that the period is proportional to the square root, or .5 power, of the length.

It also shows the reasoning we would use for frequency f, knowing that frequency is inversely proportional to the square root of the length.

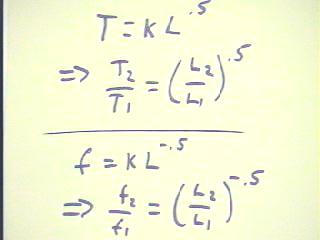
Video File #08

http://youtu.be/pto-iXVG6x8

Digression

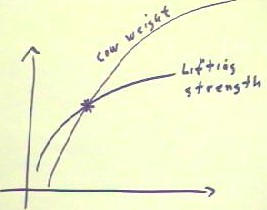
An interesting digression was provided by the student who asked about the following bit of folk wisdom: If you start off by lifting a newborn calf everyday, won't you eventually be able to lift the whole cow?

If a previously untrained individual starts lifting weights, strength will increase rapidly at first, then will begin to level off.
There is a limit how strong in individual can get, and this limit is approached as an asymptote in a more or less exponential manner.

Unless we have some sort of a Pygmy cow, its weight, which approaches its maximum weight in a similar manner, will at some point exceed the lifting strength of the individual.

We note that it is our common experience that people can't lift full-grown cows.
Even if it was, a similar argument could be made by replacing cows with elephants, or T-Rex's, or blue whales.

Video File #03

http://youtu.be/F7mWk9Sf9iQ