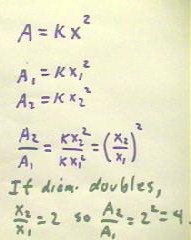
Quiz Problems
The first quiz problem asked by what factor the surface area of a sphere changes when the diameter of the sphere doubles, and by what what factor the surface area of a sphere changes when the volume of the sphere doubles.
An alternative statement of the problem asked of what factor the volume of the sphere changes when the diameter of the sphere doubles, and by what factor the volume changes when the area of the sphere doubles.
To determine the proportionality between area and volume, we begin by assuming that the proportionality is of the form of a power function, so that A = k V^p for some power p. We wish to find a power.
We can reason directly by saying that A is proportional to the square of the diameter x, or A is proportional to x ^ 2, while volume V is proportional to the cube of the diameter (V proportional to x^3).
Proceeding more formally, as we have done before, we assume that A = kA x^2 and V = kV x^3, where kA and kV are constants.
We can similarly reason that since A is proportional to x^2, x is proportional to A^(1/2).
Note also that if V is proportional to A^(3/2), it follows that A is proportional to V^(1/(3/2)) = V^(2/3)
The proportionalities between A and V are indicated below.
Using the first proportionality we see that the ratio of areas is equal to the 2/3 power of the ratio of volumes.
Solving an equation of the form x^p = c
If we have an equation of the form x^p = c, we solve by taking the 1/p power of both sides.
We apply this idea to the equation x^(2/3) = 7 below.
Brief review of first and second difference of a sequence
Recall that if a sequence is generated by a quadratic function, its first difference will exhibit linear behavior and its second difference will be a nonzero constant.
The first difference sequence S' is -19 -17 -15 ... .
Recall that if a sequence reduces to a nonzero constant sequence by a process of n differences, then that sequence can be generated by a polynomial of degree n.
"