Class Notes

Class Notes Precalculus I, 10/13/98

Review Notes for Test

In response to a question raised by a student, we find the average slope between the x = h and the x = k points of the graph of the general quadratic function y = a x^2 + b x + c.

The figure below shows the situation.

At x = h the y coordinate, or 'height', of the graph would be a h^2 + b h + c.
Similarly at x = k the y coordinate would be a k^2 + b k + c.
The rise would therefore be be

rise = a k^2 + b k + c - (a h^2 + b h + c) = a (k^2 - h^2) + b (k-h).

Since the run from x = h to x = k is run = k-h, the slope is therefore

slope = [ a (k^2 - h^2) + b (k-h) ] / (k-h).

If we factor k^2 - h^2, then divide the denominator k-h into the numerator, we finally obtain a slope of

slope = a (k-h) + b.

Figures to accompany numbered items on the Linked Outline

New items on the Linked Outline, covering material discussed since the last test, are discussed below. See also the Linked Outline.

The slope = slope equation of the straight line between two given points is obtained by setting the slope between the two points equal to the slope between the one of the points and a general point (x,y).

If the two given points are (x1, y1) and (x2, y2), then the slope between them is (y2 - y1) / (x2 - x1).
The slope between the first of the given points and the general point is (y - y1) / (x-x1).
Setting these slopes equal we obtain the equation

slope = slope equation: (y - y1) / (x - x1) = (y2 - y1) / (x2 - x1).

If we multiply both sides of this equation by (x-x1), then add y1 to both sides we will obtain the slope-intercept form of the equation.

The figure below shows the points (x1, y1), (x2, y2) and (x, y), with the appropriate slope triangles.

In this example, rather than the first given point, we find the slope to (x,y) from the second given point.
The resulting equation (y - y2) / (x - x2) = (y2 - y1) / (x2 - x1) is identical to the equation found in the preceding paragraph.
If we solve this equation for y and simplify we will obtain the same thing as if we do the same to the equation of that paragraph.

We can obtain the equation of the straight line give two points on its graph by substituting the coordinates of each point into the linear form y = mx + b.

We obtain a system of simultaneous equations.
For example, if the points are (x1, y1) and (x2, y2), we obtain the two equations y1 = m x1 + b and y2 = m x2 + b.
It should be clear that when the second equation is subtracted from the first, we eliminate b and obtain an equation we can then solve for m.
Having obtained m, we can substitute it back into either of the equations and easily solve for b.

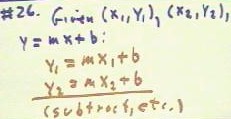
http://youtu.be/2iwrDiZsn2o

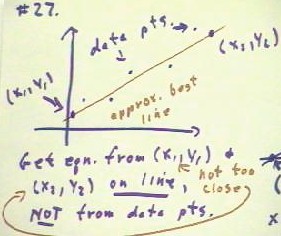
If we have a set of data which can reasonably be fit by a straight line, we can find the approximate equation of the best fit line.

We first sketch a straight line which comes as close as possible, on the average, to the data points.
We then find coordinates of two points on this straight line, not too close together, and from these coordinates determine the approximate equation of the line.

The actual best-fit linear function, which is the one given by DERIVE, is the one whose graph minimizes the square root of the average of the deviations between the function and the data point.

In this course we will not concern ourselves with techniques for finding this equation, but will simply think of the best-fit linear function as the one which comes as close as possible, on the average, to the points.

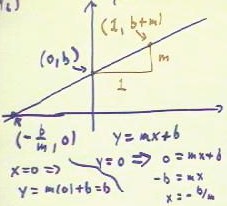
The basic points of the graph of the linear function y = mx + b are taken to be the y intercept (0, b) (which is the point where x = 0), and the point one unit to its right.

Moving one unit to the right, the run is 1; since the slope is rise / run = m, it follows that the rise must be m.
Thus the y coordinate of the point will be b + m and, since the x coordinate is clearly 1, the point will be (1, b + m).
We note that this point is higher than the y intercept when m is positive, and below the y intercept when m is negative.

We note also that the x intercept of the function y = mx + b occurs when y = 0, and is therefore found by solving 0 = mx + b for x.

We obtain x = - b/m, so the x intercept is the point (-b/m,0).
The figure below shows these points, and also shows the slope triangle used to find the point (1, b + m).

http://youtu.be/uMh1zWR-b6M

To interpret the average rate of change between two points on a graph, we note that the rate is the change in the quantity represented by the dependent variable (the rise) divided by the change in the quantity represented by the independent variable (the run).

When these quantities are divided we obtain the number of units of change in the dependent variable per unit of change in the independent variable.
In our first flow model, for example, we obtained the number of centimeters of depth change per second.
A second is the unit of change of the independent variable, and centimeters represent the units of change of the dependent variable.

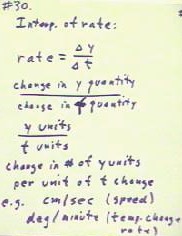
The difference equation a(n+1) = a(n) + c, a(0) = b, is evaluated for n = 0, 1, 2, 3, . . ..

Starting with n = 0, we obtain a(1) = a(0) + c; since we know that a(0) = b, we obtain a(1) = b + c.

Continuing with n = 1, we obtain a(2) = a(1) + c; since we now know that a(1) = b+c, we see that a(2) = (b+c) + c = b + 2c.

Then n = 2 tells us that a(3) = a(2) + c; having found that a(2) = b + 2c we see that a(3) = b + 3c.

The pattern that emerges is

a(0) = c,

a(1) = b+c,

a(2) = b + 2c,

a(3) = b + 3c,

. . . ,

a(n) = b + n * c.

It is clear that this pattern is linear, changing by the same amount for each subsequent value of n.

http://youtu.be/Yujiy-vEMMo

The average rate at which a function changes is given by `dy / `dx.

This rate is represented by the average slope between two points of the graph of the function.
If the function is linear, then the slope is always the same, so we have `dy / `dx = constant.

If we speak of the instantaneous rate which a function changes, we mean the rate at which it changes at a point of its graph, as the run of a series of slope triangles originating at that point shrinks down toward 0.

We then no longer speak of the average slope or average rate, but the instantaneous rate.
This rate is designated dy / dx.
It should be clear that for a linear function, this rate is again always the same, so we right dy / dx = constant.

(The figure below should be labeled #32). These equations, `dy / `dx = constant and dy / dx = constant, are called rate equations.

The first is an average rate equation and the second is an instantaneous rate equation.
Rate equations (later called differential equations) play an extremely important role in mathematics, since they allow us to express the ways in which rate change, and since these equations can often be solved to find important function models.
Solving these equations requires the use of calculus, and we will not solve them in this course.
We will, however, look at how to write certain important rate equations.

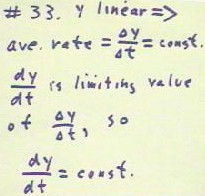
If the length of the side of the square is doubled, we obtain a square large enough to contain 4 of the original squares (two rows of two squares each). If the side of cube is doubled, we obtain a cube large enough to contain 8 of the original cubes (two layers each containing to rows of two cubes each).

As the side x of a square is changed, its area is A = x^2. As the side x of a cube is changed, its volume is V = x^3.

If x is any linear dimension of a square, that is, any dimension that can be measured by a ruler (such as its perimeter or its diagonal), then the area of the square is A = k x^2, where k is a constant that depends on which linear dimension is being measured.

We say that the area of the square is then proportional to the square of the linear dimension.

If x is any linear dimension of cube, then the volume of the cube is V = k x^3, were k is a constant which depends on which linear dimension is being measured. We say that the volume of the cube is then proportional to the cube of the linear dimension.

If two objects are geometrically similar, then if x is any linear dimension of the corresponding class of objects (e.g., the diameter of the circle, the circumference of a sphere, the radius of the base of a cone whose height is equal to its diameter), then

The surface of the second object can be 'tiled' as accurately as desired by tiny squares in exactly the same way as the first, with the sides of the squares in the same proportion is the linear dimensions of the two objects.

Furthermore, the volume of the second object can be filled as accurately as desired by tiny cubes in exactly the same way of the first, with the sides of the cubes in the same proportion is linear dimensions of the two objects.

It follows that for any class of geometrically similar objects, area is proportional to the square of a given linear dimension and volume is proportional to the cube of this dimension.

That is, area = k x^2 and volume = k x^3.

http://youtu.be/JU3FzU8_GqE

If we know that two quantities y and x are exactly related by proportionality y = k x^p (e.g., A = k x^2 or V = k x^3), then one data point (x1,y1) suffices to find the value of k.

We merely plug in the values x1 and y1, obtaining y1 = k x1^p, and solve for k. (The result is k = y1 / x1^p).
If we then substitute this value of k into the form y = k x^p, we obtain a specific function relating y to x.

If the proportionality y = k x^p is not exact, we can find a reasonably good approximation to the best value of k by substituting every data point into the form to obtain a value of k for that data point.

We then average the values of k for all the data points.
(A better alternative is to use DERIVE or another computer algebra system to find the best y = k x^p fit to the data).

The example below shows how to find k for a y = k x^3 proportionality.

x1 and y1 are to be regarded as known numbers.

To determine the best y = k x^p proportionality for the data set by using DERIVE, we use the syntax FIT([ x, k x^p], #1) for different values of p.

Using the geometry of the situation or other information to predict the best value of p, we try various values in the neighborhood of the predicted best value until the graph of the resulting fit function best matches the graph of our data.
An optimal fit will lie close to the curve and will give random residuals.

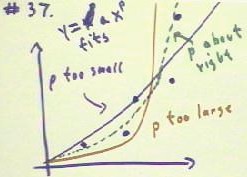
The figure below shows the data set, represented by large blue dots, and three attempts to find the right value of p for a power-function fit.

The red graph depicts a fit when the value of p is too large, resulting in residuals that lie above the graph for small values of x and below the graph for large values of x.
The blue graph depicts a fit when the value of p is too small, resulting in residuals that tend to be below the curve for small values of x and above the curve for large values of x.
The dotted green line depicts a value of p for which the residuals seem to alternate randomly between being above and below the graph; this function seems to have about the right value of p.

If y = k x^p, then

y2 / y1 = (k x2^p) / (k x1^p) = (k/k)(x2^p / x1^p) = x2 ^ p / x1 ^ p = (x2 / x1) ^ p.
This is shown in the figure below.

If y = k x^p, then

x^p = y / k and x = (y/k) ^ (1/p) = (1/k)^(1/p) * y^(1/p).
Since k is constant, (1/k) ^ (1/p) is also constant so we might as well call it k.
This k has a different value than the k of y = k x^p, but it is still constant.
We can thus say that the proportionality of x to y is x = k y^(1/p).

Since we have x = k y ^ (1/p), we have

x2 / x1 = (k y2^(1/p)) / (k y1^(1/p)) = ... = (y2 / y1) ^ (1/p), where the intermediate steps are identical to those used previously.

Thus, given the ratio of two x values we can obtain the ratio of the corresponding two y values, and given the ratio to y values we can obtain the ratio of the corresponding x values.

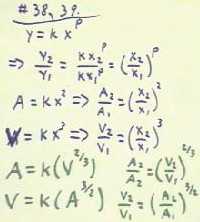
For most real objects the surface areas of geometrically similar objects are proportional to the square of linear dimension, and volumes are proportional to the cube of linear dimension.

We could write this as area = kA x^2, and volume = kV x^3, where kA and kV are understood to be different proportionality constants.

To get the proportionality of area to volume, we can solve the volume proportionality for x, obtaining

x = (volume / kV) ^ (1/3), and then substitute this into the area proportionality.

We will obtain area = kA * [ (volume / kV) ^ (1/3) ] ^ 2 = kA * (volume / kV) ^ (2/3) = (kA / kV^(2/3) ) * volume ^ (2/3).
The expression (kA / kV ^ (2/3) ), which since kA and kV are constant must also be a constant, can simply be called k, and we have the proportionality

area = k (volume) ^ (2/3).

We can follow similar procedure, this time solving the area proportionality for x and substituting into the volume proportionality, to obtain

volume = k (area) ^ (3/2), where the value of k is different than in the previous proportionality.

It will follow that for two geometrically similar figures, the ratio areas for two given volumes will be

area 2 / area1 = (volume2 / volume1) ^ (2/3), while the proportionality of volumes for two given areas will be
volume2 / volume1 = (area2 / area1) ^ (3/2).

These relationships are summarized in the figure above.

http://youtu.be/BFiQmZhDdhI