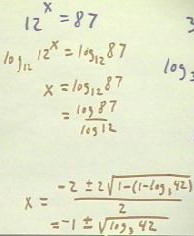"
Class Notes Precalculus I, 11/03/98
Logarithms; Modeling Exponential Behavior
The first quiz problem was to solve the equation 12 ^ x = 87.
- We do this by taking the base-12
log of both sides.
- The inverse function property
tells us that log {base 12} (12 ^ x) is x, while the laws of logarithms tell us that
log{base 12} (87) is log(87) / log(12).
- We can evaluate this expression to
find x. (The quadratic equation solution at the bottom of the figure is irrelevant here).
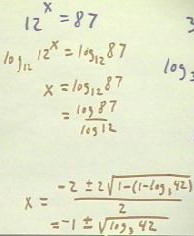
The second quiz problem was to solve the equation 3 ^ (x^2 + 2x + 1) = 42.
- This time we take the base-3 log of both sides, obtaining the quadratic equation in the
third line below.
- In order to get an exact solution to the equation, we do not approximate the base-3 log
of 42, but we treat this expression as a constant.
- We thus solve the quadratic equation by first subtracting this log from both sides,
including it with the other constant term, 1, on the left-hand side.
- We see that we have a quadratic equation with a = 1, b = 2 and c = 1 - log{base 3}(42).
- Note again that c is just a number; we can approximate it to many decimal places anytime
we wish, but for now we keep it in its exact form.
- Plugging these numbers into the quadratic formula, we obtain the fifth line below; in
the sixth line all we do is express 2^2 as 4.
- At this point we return to the bottom of the figure above, where this expression for x
is simplified.
To get the first expression we factor 4 out of expression under the the square root,
then take the square root of the 4. (Note that it would have been simpler to just
distribute the multiplication by -4 under the square root, then let the 4 and resulting -4
cancel).
- Dividing through the resulting numerator by the denominator we obtain x = -1 +-
`sqrt(log{base 3}(42)), which again can be evaluated to any desired degree of accuracy.
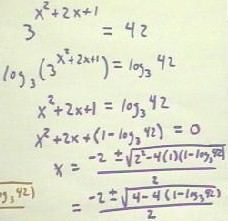
Video file #01
http://youtu.be/-V0fNX2yOoM
Modeling temperature T vs. time t
We now proceed to obtain an exponential model corresponding to the temperature T vs.
time t data for the Brussels sprout (at the end of the last worksheet).
- Estimating from this graph we obtain approximate points (7, 65) and (40, 35).
- From the data points at the largest shown values of t, which represent temperatures
after the temperature programs removed from the sprout, we see that the room temperature
is about 27; the exponential function will approach this temperature as a horizontal
asymptote.
- Our exponential model will be T = Td0 b^t + c, where Td0 is the original value of the
temperature difference Td between the sprout and the room, and c is the value of T
approached as an asymptote.
- Thus we see that c = 27.
- If we graph Td vs. t, the asymptote will be Td = 0, since the temperature difference
between the sprout in the room approaches 0.
The temperature difference Td corresponding to the point (7,65) is 65 - 27 = 38,
representing the difference in temperature between the sprout in the room at t = 7.
We thus have the point (7,38) on the graph of Td vs. t.
Similarly the point (40,35) represents a temperature difference of 35 - 27 = 8, and uses
point (40,8) on the graph of Td vs. t.
- Assuming that Td = Td0 b^t, consistent with the exponential model we are using, we can
substitute our data points into this function to determine Td0 and b.
We obtain the equations 38 = Td0 b^7 and 8 = Td0 b^40, as shown below.
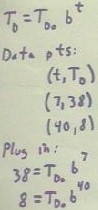
Video file #02
http://youtu.be/FYW6Jff2M48
To solve these equations we divide the top equation by the bottom.
- We obtain 38 / 8 = b^7 / b^40, or b^(-33) = 4.75.
- We have several choices of how to solve this equation.
- In the figure below we take the logarithm of both sides of the equation, obtaining on
the left -33 log(b) (using log(x^y) = y log x) and on the right log(4.75).
- Solving for log b, we obtain log b = - log(4.75) / 33.
- Using the inverse function law of logarithms, we translate this to b = 10^( - log(4.75)
/ 33), which we easily evaluate using a calculator.
- We obtain b = .954 (approximately).
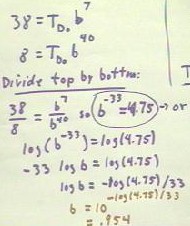
Alternatively, as shown below, we can solve b ^ (-33) = 4.75 by taking the -1/33 power
of both sides.
- b^(-33) ^ (-1/33) = b^(-33 * -1/33) = b^1 = b, so we see that b = 4.75 ^ (-1/33).
- We easily evaluate this to obtain b = .954, as before.
- Whichever means we used to find the value of b, we can now substitute b into the first
of the equations to obtain 38 = Td0 (.954) ^ 7.
As shown below this is easily solved to obtain Td0 = 52.8.
Our model therefore becomes Td = Td0 b^t = 52.8 (.954) ^ t.

Since for this model the actual temperature T is Td + 27, we therefore have temperature
function T = 52.8 (.954) ^ t + 27.
- We can compare values of this function with the values observed on the graph.
- The graph shows that at t = 25, the temperature is approximately 41 (a more accurate
estimate might be 42).
- Evaluating the model at t = 25, we obtain T(25) = 43.3, which is not too far from 41 and
even closer to 42.

Video file #03
Another strategy suggested for solving the original equations was to first takes a log
of both sides.
- This solution, which does a good
job of demonstrating several of the laws of logarithms, is shown below.
- The third line from the bottom of
the figure below is essentially identical to a line we obtained in our first solution for
b.
- We obtain the same value for b as
before.
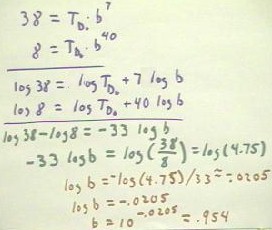
Video file #04
http://youtu.be/Pi_o3XYCGxU
"