"
Class Notes Precalculus I, 11/05/98
Linearizing Exponential Data; Introduction to Polynomials
The first quiz problem was to obtain a model of a form y = A b^x for the two (x, y)
data points (8, 12), (15, 9).
- Substituting the values of x and y from the two data points, we obtain the equations 12
= A b^8 and 9 = A b^15.
- We could solve these equations by any of several methods.
- We could for example solve the first equation for A and substitute the resulting
expression into the second equation.
- We would then substitute our solution of this equation back into the first, to obtain an
equation we could solve for the second.
- Or we could solve one of the equations for b and substitute the result into the second,
and then proceed similarly.
- In this case we will divide the first equation by the second; it will quickly become
apparent that this strategy will eliminate A from the system.
- The steps are shown below.
- Between the fourth and fifth
lines, we see that A / A = 1, so A b^8 / (A b^15) = b^-7.
- We then take the -1/7 power of
both sides to obtain b.

We proceed to substitute this value of b into the first of the original equations and
solve for A.
- By straightforward steps, shown below, we obtain A = 16.6 (approximately).
We thus have A = 16.6 and b = .96.
- It follows that our model is y(x) = A b^x = 16.6 (.96) ^ x.
The quiz asked us determine the value of y when x = 30 and of x when y = 100.
- To obtain the value of y when x = 30, we evaluate y(30), obtaining an approximate value
of 5, as shown below.
- To obtain the value of x when y = 100, we first substitute 100 for y to obtain the
equation y = 16.6 * .96^x (incorrectly written below as y = 16.9 * .96 ^ x).
- To solve this equation for x, we first divide both sides by 16.6 to obtain .96 ^ x = 5.9
(approximately).
- We then take a base .96 logarithm
of both sides to obtain x = log (5.9) / log(.96), which we can easily evaluate using a
calculator.
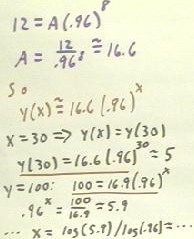
Video file #01
http://youtu.be/oixX06DucEI
Fitting an exponential function to data
As we have seen previously, we can fit an exponential function to two data points if we
know the value the function approaches as an asymptote.
- However, even if we know what the asymptote should be, if we have a large number of data
points we must still choose two points to represent all the data.
- Our model is therefore subject to our choice, as well as to errors in the data.
- When we choose only two points, we do not effectively average the behavior of all the
points.
- A better approach would be to fit a function to all the data, as we have done using
DERIVE with linear, quadratic and power function data.
- However, DERIVE does not allow us to use a fit function that has the variable in the
exponent (or within any other function except mostly those made up from a sum of power
functions).
Consider the y vs. x data below.
- Before they were scratched out, we can see that the y values had a common ratio of 2.
- Since the x values changed by 1 each time, this is tells us that y is in fact an
exponential function with base 2.
- We have replaced the scratched-out values with values which are close to, but not equal
to those values.
- Since the 'new' y data are nearly exponential, we expect that we can find an exponential
function which does a good job of approximating those values.
- If we did not know in advance that this data should be nearly exponential, we would have
a harder time seeing that the behavior is exponential.
- For example, a quick glance at the
data won't tell us whether an exponential function is more appropriate than a power
function.
- In such a case we might try both exponential and power-function models.
If we choose to attempt an
exponential model, we can proceed as follows:
- We attempt to linearize our
function by an appropriate transformation.
- We will then obtain a linear fit
to our transformed data.
- Finally we will iinverse-transform
our linear function to obtain a model for the original data.
- It appears that the y values are
approaching 0, so we will assume asymptote 0.
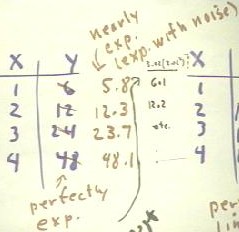
To linearize an exponential function we use the transformation y -> log(y),
in which we replace all our y values with log(y). The table below
shows the resulting log(y) vs. x data.
- First observe what would have happened with our original perfectly exponential data:
- Had we applied the transformation y -> log(y) to our original scratched-out data, we
would have obtained the scratched-out column for log (y) in the figure below.
- You should validate this, then figure out for yourself why it is obvious that this table
(using the scratched-out data) would be perfectly linear.
- The table with the scratched-out data is is perfectly linear because the x data are
separated by equal intervals and because the log(y) column is also separated by equal
intervals (in this case the interval is very nearly .3).
- A linear function will therefore fit our scratched-out data
- Now we transform the actual 'noisy' data. We obtain the second (red) log(y)
column, as you should verify.
- The log (y) data now has
differences .33, .28 and .31 corresponding to equally spaced x values.
- Thus log(y) vs. x is not perfectly
uniform but is nearly so.
- We are therefore encouraged to go
ahead and find a linear model for log (y) vs. x.

Our linearized model will thus be a model for log(y) vs. x.
This model is represented by the log (y) vs. x graph below.
- As usual, after plotting our points we choose two points on the approximate best-fit
straight-line and use them to determine the equation which models the data.
- We obtain the estimated equation log (y) = .305 x + .48 (approximately).
- Alternatively we could have used an appropriate calculator or a computer algebra system
to obtain the equation for the best-fit line.
We now have an equation which models our transformed data, log(y) vs. x.
We need an equation to model our original y vs. x data.
We return our model to the
original y vs. x by inverting the transformation y -> log(y).
- To invert the transformation, we
solve our equation for y.
- Recalling the law of logarithms
that states that log(y) = x is equivalent to 10^x = y, which constitutes the original
inverse-function definition of the logarithm function, we obtain the equivalent equation
- By the laws of exponents (x ^ (a +
b) = x^a * x^b) we see that the right-hand side can be expressed as 10^.305x * 10^.48;
since 10 ^ (.305 x) = (10 ^.305) ^ x = 2.02 ^ x and 10 ^.48 = 3.02, we finally obtain
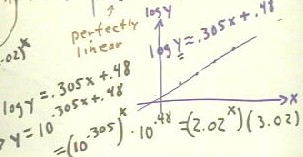
We now compare the values obtained for the given x values using the function y = 3.02
*2.02 ^ x to the original 'noisy' data from which the model was obtained.
We hope that our function values
are close to the original data, and that there is no clear pattern to the residuals.
If this is the case we have some confidence in the quality of our model.
- We evaluate our function for x =
1, 2 ,3, and 4, and compare these values to the corresopnding data values 5.8, 12.3, 23.7,
and 48..
- We obtain the values shown in the
table below.
- For x = 1 we obtain y = 3.02 *
2.02 ^ 1 = 6.1 (approximately).
- For x = 2 we obtain y = 3.02 *
2.02 ^ 2 = 12.2 (approximately)
- We could then obtain the x = 3 and
x = 4 values which you should calculate yourself and compare to the data values.
- The function fits the data very
well, sometimes being somewhat greater and sometimes somewhat less than the data but never
differing by more than a few tenths of a unit from the data, and with no clear progression
in the residuals.
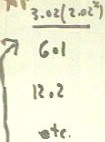
The figure below shows the entire process.
- The process starts with the
original data in the upper left-hand corner of the figure, moves to the transformed data
in the upper right, then to the linear fit at lower right and the application of the
inverse function 10^x to 'undo' the logarithmic transformation, and finally back to the
upper right where the function values are compared to the data values.

Video file #02
http://youtu.be/M_X7J3AOrQ4
Had we not known that the data was obtained by inserting random errors (sometimes
called 'noise') into exponential data, we might also have attempted a power-function
transformation.
- For example, we might for some reason have attempted a y -> y^.6 transformation.
- The result would have been the y ^ .6 vs. x table shown in the middle of the figure
below.
- Our transformed data would not be particularly linear the graph of the y ^ .6 vs. x
points exhibits a gradual and consistent upward curvature.
- A y ^ .5 or y ^ .4 transformation would probably have been more nearly linear.
- However, it is possible that random errors in data could result in such a slight
linearity even though the behavior being observed should in fact be linearized by this
transformation.
- So we proceed to sketch a straight line attempting to model the data points (the
straight line sketched below doesn't do a particularly good job of this; a DERIVE fit
would do a much better job, as would anyone with a good eye and a straightedge).
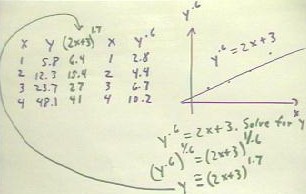
The estimated fit for the transformed data gives us y^.6 vs. x.
- The linear functoin seems to have slope 2 and y-intercept 3.
- The transformed function is therefore y ^ .6 = 2 x + 3.
- We solve this for y by taking the 1/.6 power of both sides, obtaining the model y = (2 x
+ 3) ^ 1.7 (approximately).
We compare our model to the original data:
- We create a column for the function y = (2x + 3) ^ 1.7 in our original table of y vs. x,
and evaluate this function for x = 1, 2, 3 and 4.
- The table shows the values we obtain.
- We see that the values give us a reasonable but not overly accurate approximation to the
observed data.
Had we attempted both the preceding logarithmic and the present .6-power transformation
of our data, with the resulting models y = 3.02 * 2.02^x and y = (2x + 3) ^ 1.7, we would
be interested in which model fits the functon better.
- The near-linearity of the graph of log (y) vs. x, the better fit of the resulting
function to the original data, and the apparent pattern of the residuals in the second
model would clearly indicate that the first of these models is by far the better.
- We would therefore choose the exponential model.
Sometimes we have to choose between competing models without a clue as to which model
should in fact be the better.
- Often, however, we have a good
idea what sort of function would be expected to model to behavior of the system we are
observing, and this can also be helpful in deciding which model to try first and in
choosing between different models.
Video file #03
http://youtu.be/qSGJdKPSCsM
As we saw with the temperature function, exponential functions do not always have the
horizontal axis as their asymptotes, and must therefore be represented by functions of the
form y = A b^t + c, with c not equal to 0.
- Such a function cannot be linearized by a logarithmic transformation, since log ( A b^t
+ c) cannot be simplified to a linear function of t (the laws of logarithms don't permit
us to do anything with the log of the sum of two quantities).
In this case, if we know the value of the horizontal asymptote y = c, we can form the
function yDiff = y - c = A b^t and fit an exponential to this function.
- Having obtained a model for yDiff, we can add back the quantity c to obtain a model for
our original data.
- This was in fact the strategy we followed for the temperature vs. clock time data
obtained for the Brussels sprout.
We will often wish to determine whether the yDiff = A b^t function is appropriate.
- Recall that the ratios of an exponential sequence are constant.
- If our y vs. t data are in fact nearly exponential, if the t values are equally spaced
the y values will form a sequence whose difference sequence should have a constant ratio.
- If the data is 'noisy', with random errors, then if the errors are not too drastic
compared to the differences in the t values, the difference sequence will have a nearly
constant ratio.
A brief introduction to Polynomial Functions and their behavior
Consider the function y = (x - 3) (x + 5) (x -7).
- We observe that this function is composed of linear factors--linear functions multiplied
by one another--and that when the linear functions of this model are multiplied together
using the distributive law we obtain a function of the form y = a x^3 + b x^2 + c x + d.
- Such a function is called a polynomial function.
- This present polynomial function is a sum of the power functions a x^3, bx^2, c x^1 and
d x^0.
- The powers involved are all integers and are all either positive or 0.
-
A polynomial function is a function formed by adding power functions with
non-negative integer powers.
A product of linear factors always gives us a polynomial function.
- Any function which is a sum of power functions for non-negative integer powers of the
variable is a polynomial function.
- The highest power represented is said to be the degree of the function.
- The polynomial function in the above example is of degree three.
It will turn out that any polynomial function is a product of linear factors
and irreducible quadratic factors
- Irreducible quadratic factors are quadratic factors of the form a x^2 + b x + c for
which there is no solution to the equation a x^2 + bx + c = 0; we will see shortly what
this means.
We attempt to graph the present function.
- We begin by asking where the zeros of the function are.
- It should be clear that, for example, if x = 7 we will have y = 0.
- This is because when x = 7, the factor (x - 7) will be 0, which will make the entire
product zero.
- We see similarly that x = 3 and x = -5 are also zeros, and we indicate these zeros on
the x axis of the graph in the figure below.
- We observe also that no other value of x can possibly give us a zero, since for any
other value of x none of the factors will be 0 and their product will hence not be 0.
- We next find the y intercept of the graph.
- The y intercept occurs when x = 0.
- Substituting x = 0 into the definition of the function we obtain y = 105.
We also observe that whenever x is a very large negative number, each of the factors (x
- 3), (x + 5), and (x - 7) is a large negative number and their product will therefore be
a really, really, really large negative number.
- This tell us that the graph must approach the 0 at x = -5 from the left through large
negative values, indicated by the purple arrow pointing downward at the lower left of the
graph.
A similar observation related to very large positive numbers tells us that for large
positive numbers, the product of the factors will be a very large positive number,
indicated by the purple arrow pointing upward toward the upper right of the graph.
- When these behaviors are combined, we obtain a graph much like that in the figure below.
- Actually, this graph isn't the best possible graph, because it is very unlikely that the
y intercept (0,105) will coincide with a 'peak' of the function.
- Plotting a variety of such functions using DERIVE will give you some intuition about how
these functions behave.
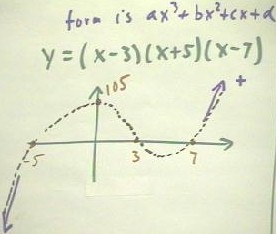
The function y = (x - 3) (x ^ 2 + 2 x + 12) is also a polynomial of degree three, since
it multiplies out to the form a x^3 + b x^2 + c x + d.
- However, the graph of this
function is somewhat different than the graph of the function in the preceding example.
- This is because, while the factor
(x - 3) still gives us a zero at x = 3, the other factor does not give us any zeros.
- We don't get any zeros from the
quadratic factor because the zeros of this factor are x = [ -2 +- `sqrt(2^2 - 4 * 1 * 12)
] / 2(1); the quantity of which we are taking the square root is in this case -44, so
there are no real zeros.
- We thus say that the quadratic
factor in this function is irreducible.
- We use this terminology because if
we can factor, or reduce, a quadratic expression, we will get two linear factors and hence
two zeros.
- Since there are no zeros
associated with the irreducible quadratic, we cannot factor it.
- The graph of this function will
therefore contain its only zero at x = 3.
- The y intercept is easily found to
be at y = -36.
- The behavior at extremely large
negative values of x and at extremely large positive values of x is seen to be the same as
before.
- We therefore obtain a graph
something like the one shown below.
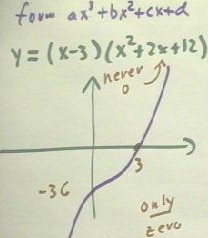
Video file #04
http://youtu.be/mU9_L-VlHUw
http://youtu.be/QHx5CbAwwg4
"
