Graphs of Polynomials

Class Notes Precalculus I, 11/13/98

Graphs of Polynomials

The quiz problem was to graph the function (x - 3) (x² - 5x + 6)(x² + 2x + 20).

We begin by attempting to completely factor the expression defining the function.
The first quadratic clearly factors into (x - 3)(x - 2).
The second quadratic has no zeros (when we set the expression equal to 0 and use the quadratic formula we get -76 under the radical) and therefore cannot be factored.
We can see that factorization is in this case impossible because if the expression did factor there would be corresponding zeros, which would contradict the results of the quadratic formula.

The completely factored form of the quadratic is the expression in the second line of the figure below.
In the third line we note that we have three linear and one irreducible quadratic factors.

From the factors we see that the zeros of this function are 3, 3, and 6.

The y intercept is easily found to be 360 by substituting 0 for x.
The far left behavior is negative, since a very large negative number would give us three negative factors, corresponding to the three linear factors, and one positive factor corresponding to the irreducible quadratic (the x² term dominates this expression when the magnitude of x is large).
For large positive values of x, the expression will give us a very large positive result, so the far right behavior is positive.

In the figure below we examine the relationship between the solutions of a quadratic equation and the factors of a quadratic polynomial.

We know that x² - 5x - 6 factors as (x - 6) (x + 1), and that this implies zeros at x = -1 and at x = 6.
If we set the expression equal to zero and use the quadratic formula, we obtain zeros 6 and -1, in agreement with the zeros we got when we factored the expression.
Had we not known the factors of the expression, the results of the quadratic formula would have told us that the factors must be (x - 6) (x + 1).

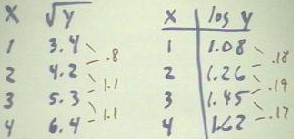
If we apply the same reasoning to the expression x² - 5x - 7, which we cannot easily factor, we would obtain zeros at x = 2.5 + `sqrt(53) / 2 and x = 2.5 - `sqrt(53) / 2 .

Our conclusion would therefore be that x² - 5x - 7 = (x - (2.5 + `sqrt(53) / 2) ) (x - (2.5 - `sqrt(53) / 2) ).

Returning to the task of graphing the function, we see that the zeros are at x = -1, 3, 6, the y intercept is at y = 360, and that the far-left and far-right behaviors are negative and positive, respectively.

Having indicated these characteristics on a graph, it becomes easy to sketch an approximate graph of the polynomial.

Video file #01

http://youtu.be/TbETIytBYZ0

We now change the function slightly, as indicated below.

The factorization of the function in this case becomes (x - 3)² (x - 2)(x² + 2x + 20).
We note that (x - 3) now appears twice in the factorization. We ask what effect this might have on the shape of the graph near x = 3.
If x is close to 3, then the factors (x - 2) (x² + 2 x + 20) will give us a value near 35.

In that case the polynomial will be approximately equal to (x - 3)² [35] = 35 (x - 3) ².

A graph of this expression is just a parabola with vertex at x = 3 (beginning with the function y = x², we vertically stretch by factor 35 then shift three units to the right).

It follows that if we graph the function y = 35 (x - 3)² and the function (x - 3)² (x -2) (x² + 2 x + 20) near x = 3, the graphs will be close to one another, becoming closer and closer as x gets closer and closer to 3.
The figure below depicts such a graph.

Using DERIVE, we authored both of these functions and plot them near x = 3.

The graph we obtained is very similar to the one sketched here, except that instead of being shifted slightly to the right of the 'red' parabola the blue graph would be shifted slightly to the left.
You should check this out using DERIVE.

Video file #02

http://youtu.be/0mTqhhKcwgs

Video file #03

http://youtu.be/96oCE4YBiPQ

The graph of the function is thus constructed by

locating the zeros and the y intercept,
noting the far-left and far-right behaviors, and recalling that
because the zero at x = 3 is the result of not one but two factors (x -3) the graph should therefore act like that of a quadratic function near x = 3, we obtain the graph below.

A DERIVE plot confirms this overall shape for the graph. However, on a scale where the y intercept is visible the 'hump' between x = 2 and x = 3 does not rise nearly as high as it does on the graph shown below.

You should confirm this using DERIVE.

We can extend the insights we have gained here to the function y = (x + 5)³ (x - 2) ² (x + 2).

We see that the zeros are at x = -5, x = -2, and at x = 2.
The zero at x = 2 will be quadratic in nature while that at x = -2 will be linear in nature.
The zero at x = -5 will act like a cubic function c * (x + 5)³, where c stands for the value of the product of the remaining factors at x = -5.

The graph shown below depicts all these behaviors, as well as the y intercept y = 1,000 and the fact that the far-left and far-right behaviors are both positive.

Video file #04

http://youtu.be/-oykSMMGAwg