Combining Functions: Ball down Incline and onto Floor

Class Notes Precalculus I, 11/19/98

Combining Functions: Ball down Incline and onto Floor

We begin with a simple demonstration of an optimization situation.

A ball rolls all the way down a grooved ramp of length L, with one end of the ramp at the edge of a table 96 cm above the floor.
The ball leaves the ramp and follows a parabolic path to the floor.

The ball is rolled again and again, with the raised end of the ramp supported at a higher and higher position with each roll. Two contrasting influences determine how far the ball travels in the horizontal direction before striking the floor:

As the high end of the ramp is raised higher and higher from the horizontal, the ball goes down faster and faster, which tends to make it strike the floor further and further from the base of the table.
However, the angle at which the ball leaves the ramp gets steeper and steeper, which tends to make the ball strike the floor closer and closer to the base of the table.

When the height h to which the far end of the ramp is raised above the tabletop is relatively small, and the angle of the ramp with respect to the horizontal direction is therefore relatively small, the change in angle has little effect on the path of the ball while the change in the elevation h of the high end has a more significant effect on the speed of the ball.
Then we find that a little increase in h will result in an increase in the distance x, the distance between the base of the table and the position at which the ball strikes.

On the other hand when the elevation h is large and the angle of the ramp with horizontal is closer to 90 degrees, a little increase in h doesn't result in much change in the velocity of the ball, and the changing angle results in a decrease in the distance x.

So we pose the problem: To what height h should we raise a ramp 63 cm long in order to maximize the distance x?
In fact we did better than just posing the problem. We actually observed the situation, and found that when the ramp was raised to a height somewhere between 32 cm and 36 cm, the distance x was greatest.

Physics can be used to obtain a function x (h) for the horizontal distance traveled by the falling ball.

While we will not discuss the physics, we will use mathematical functions to obtain this function.
In the process we will encounter a variety of ways to combine functions.
And we will get to see if our mathematical analysis predicts the same results we saw in class.

We won't go over the physics of the situation here, but physics tells us that the initial velocity of the ball should in the most ideal of conditions be

initial ball velocity, most ideal conditions: v₀ = `sqrt(2 * 980 * h),

where v₀ is measured in cm/second whenever h is measured in cm.

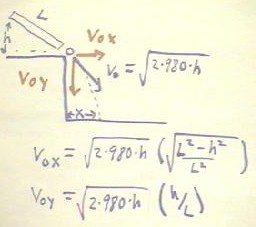
The velocity v₀ can be tracked in two directions.

The ramp makes a triangle with the horizontal and vertical directions. The sides of the triangle are

the length L of the ramp (the hypotenuse)

the altitude y of the ramp (the vertical side) and

the horizontal side, whose length is by the Pythagorean Theorem `sqrt( L² - y² ).

The initial velocity of the ball is in the same direction as the ramp, so the vertical and horizontal comonents of the velocity are in the same proportion to the ball's speed as the vertical and horizontal sides of the triangle to the length of the ramp.

In the horizontal, or x direction, the ball will therefore be moving at velocity v_0x = `sqrt( 2 * 980 * h) * `sqrt( [L² - h²] / L² ).
In the vertical, or y direction, the ball will be moving at velocity v_0y - `sqrt( 2 * 980 * h) * ( h / L ).

These velocities are indicated in the figure below.

These expressions can be simplified considerably, and will be. They are left in their present form to indicate to anyone with a reasonable background in physics how they were obtained. For anyone with such a background, we give the following brief explanation:

(Physics: may be safely ignored):

The initial velocity v₀ is obtained by setting the kinetic energy gain equal to the potential energy loss of the ball on the ramp, assuming that the ball starts from rest.

The quantities by which v₀ is multiplied are simply the sine and cosine of the angle made by the initial velocity with horizontal, as obtained by similar triangles with the aid of the Pythagorean Theorem.

We will use the standard analysis of projectiles to determine the range x.

The distance x at which the projectile strikes will be the horizontal distance traveled by the ball from the edge of the ramp to the floor.

The horizontal velocity of the ball doesn't change, so the horizontal distance will simply be the product of the constant x velocity and the time required to reach the floor.
Since the x velocity is constant, it is equal to the expression v_0x already obtained, so if `dt is the time required to reach the floor, we have x = v_0x * `dt.
Using the quadratic function that describes the altitude y as a function of clock time, we obtain the quadratic equation 96 = v_0y `dt + 490 `dt² for the time `dt required to fall.

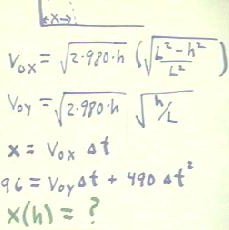
We see that for a given ramp length L, v_0x is a function of h, which we could write v_0x(h) to emphasize this functional dependence. Similarly, v_0y will be a function of h, so we write v_0y (h) to indicate this function.

Now, `dt depends on v_0y (the faster the ball is going down at the start, the shorter the time required to fall).
Since `dt depends only on v_0y and v_0y depends only on h, ultimately `dt depends on h.

Where does this leave us? Well, remember that we were trying to find the distance x as a function of the height h to which the raised end of the ramp was lifted above the table.

The desired distance x is the product of the function v_0x (h) and `dt.
This function is also ultimately a function of h, since as we just saw `dt depends on h.

So all we have to do to find x = v_0x (h) `dt is solve the quadratic equation for `dt, plug in our function v_0y (h) for v_0y, then put the result together with our expression for v_0x (h) and we will have our function x (h).

The scheme is fairly simple. However, be warned. The algebra is really messy.

Just don't let the messy algebra distract you from the fact that we are just trying to do three things:

solve a quadratic for `dt,

substitute for v_0y, and

put our expressions together to get x = v_0x * `dt.

Doing the messy algebra

We begin by solving the quadratic, which is something we are pretty familiar with.

We rearrange the equation for `dt into the form 490 `dt² + v_0y `dt - 96 = 0, then use the quadratic formula with a = 490, b = v_0y and c = -96.
We obtain the solution in the second line.

In the third line we choose the + of the +- from the second line.
We choose this because we want `dt to be positive, and since `sqrt( v_0y² + 190,000 ) > `sqrt( v_0y² ) = v_0y, we are assured that -v_0y + `sqrt( v_0y² + 190,000 ) will be positive.
Note also that the 190,000 is an approximation of the product -4 * -96 * 490.

In the fourth line we note that v_0y = `sqrt( 1960 h^3 ) / L.

We can obtain this as follows:

v_0y = `sqrt( 2 * 980 h ) * h / L

= `sqrt (1960 h) * `sqrt(h²) / L

= `sqrt (1960 h * h²) / L

= `sqrt( 1960 h^3 ) / L.

In the fifth line we substitute this expression for v_0y into our solution for `dt, obtaining the expression in the last line.

Video File #02

http://youtu.be/jLq4oK2l-W4

Video File #03

http://youtu.be/Dpf7HZ7DcTk

We continue the algebra below.

The first line is just the last line of the preceding figure.
In the second line we simply square the first term under the second square root, obtaining 1960 h^3 / L ².
In the third line we have eliminated denominators from the numerator by multiplying both numerator and denominator by L.

Note that when we multiply the expression under the second radical by L², we are in fact multiplying the radical by L.

Video File #04

http://youtu.be/5WMKm6H1Mj8

We now continue the adventure by multiplying our last expression for `dt by our expression for v_0x.

We easily obtain the second line in the figure below. Then the fun begins.

In the third line we have used the fact that 1 / L is a factor of the numerator, and hence of the entire fraction, so that the denominator becomes 980 L ².

In the fourth line we combine the expressions under the two radical factors that begin the numerator:

`sqrt( 1960 h) * `sqrt ( L² - h² ) = `sqrt ( 1960 h ( L ² - h ²) ).

This could be further simplified by distributing the multiplication through the subtraction, but this step will be saved for later.

In the last line of the figure we distribute the multiplication in the numerator through the addition.
Since every multiplication involves multiplying two square roots, we combine each of the two terms of the numerator under one square root.

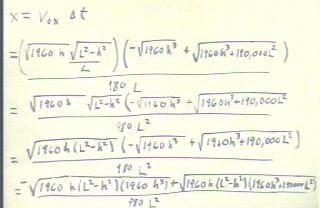
Video File #05

http://youtu.be/mq-WWJcQzE4

We then note that each term of the numerator has 1960² as a factor under the radical.

We can thus factor out `sqrt(1960)² = 1960 in the numerator.
Noting that 1960 / (980 L²) = 2 / L², we are left with the expression in the second line.
We then factor out h² from the first term, while under the square root factoring h^4 from the first two terms and 96 L² h from the second two.
We see that `sqrt(L² - h²) is common to every term of the expression, and in line 4 we factor this quantity out.
In the fifth line we replace the 96, representing the altitude of the low end of the ramp above the floor, with y0 in order to accomodate the model to different possible altitudes.

Students viewing video clips note: the - on the first term got lost in the version seen in the clip. The expression below is the correct one.

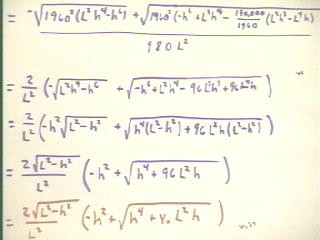
Video File #06

http://youtu.be/knjuVvj-Xks

Video File #07

http://youtu.be/3LKtq2GeKr8

We thus finally have the function

x(h) = 2 `sqrt( L² - h² ) / L² [ - h² + `sqrt ( h^4 + y0 L² h ) ].

This function is made up of square roots of polynomial functions, where the variable in the polynomials is h.

We have combined functions in a variety of ways to get this result.

We have taken square roots of polynomials,
we have added functions,
we have multiplied functions.

For the specific ramp where L = 63 and y0 = 96, we have the function

x(h) = 2 `sqrt( 63² - h²) / 63² [ -h² + `sqrt ( h^4 + 96 (63²) h) ].

In class we observed that when h was 36 cm, x(h) was around 60 or 70 cm.

Plug these numbers for h into the function and see if the model is close. That is, for h = 36 cm, do we get x = 60 to 70 cm?

You should then graph the function, using DERIVE or some other computer algebra system, and see where the maximum distance occurs and what it is.

Note that this model is a simplification of the real situation.

The model did not account for such things as friction or the rotational kinetic energy gained by the ball as it rolled down the ramp.

The model will therefore differ significantly from the actual function governing the situation, though it will accurately show the general overall behavior of the real x(h) function.

Below we recapitulate the process of our solution.

We started with the functions v_0x (h) and v_0y (h), noting that both are functions of h.
We then solved the quadratic equation for vertical motion to obtain `dt as a function of v_0y, as indicated in the third line below.
In the fourth line we note that sinse v_0y is a function of h, `dt ( v_0y ) is a function `dt ( v_0y (h) ), which is ultimately a function of h.

In the last two lines we substitute the function v_0y (h), indicated in red, into the expression for `dt, obtaining once more the expression for `dt in terms of h.

We can now say that `dt is a function `dt (h).

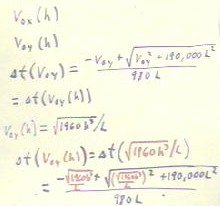
We finally substituted our expressions for v_0x (h) and `dt (h) to obtain the function x (h).

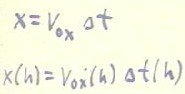
As we saw earlier in the semester, the function `dt ( v_0y (h) ) is a composite function, the composite of `dt ( v_0y) and v_0y (h).

The function x(h) = v_0x (h) `dt (h) is a product of two functions, and is therefore called, not surprisingly, a product function.

Video File #08

http://youtu.be/MtA6N5KnJr4