We begin with a model of rabbit populations. We start with 1 pair of baby rabbits, and use the following premises:
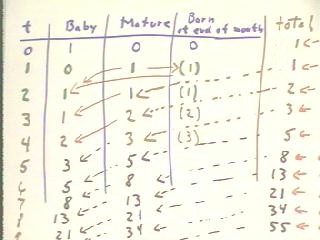
The table below keeps track of the number of pairs of baby rabbits, mature rabbits, and total rabbits versus the number of the month since we began. We also have a car that shows the number of rabbits to be born at the end of the current month. Numbers in this column will be written in parentheses because the rabbits will really be counted until the beginning of the next month.
We see that at the beginning, when t = 0, we have one pair of baby rabbits and zero pairs of mature rabbits. Since the only rabbits we have are babies, no rabbits will be born at the end of this month and the total number rabbit pairs is 1.
Therefore at the beginning of the next month, when t = 1, we have no new baby rabbits. The one pair of baby rabbits from the previous month will have matured so we will have 1 pair of mature rabbits. As a result 1 pair of baby rabbits will be born at the end of this month; this number is listed in parentheses and not counted as part of the total until the next month.
It follows that at the beginning of the next month, when t = 2, we have 1 pair of just-born baby rabbits. Our mature rabbits from the previous month, of course, are still around and ready to begin the reproduction cycle once more. Therefore at the end of the month we will have another new pair of baby rabbits. Our total number of rabbit pairs will now be 2.
Now at t = 3 we have the pair of baby rabbits just born, 2 pairs of mature rabbits (the previous mature pair plus the pair that were babies in the previous month). As a result of the 2 mature pairs we will have 2 pairs of baby rabbits at the end of the month. Again not counting these two pairs of baby rabbits, we have a total of 3 pairs of rabbits.
At t = 4 we have the two new pairs of baby rabbits, 3 pairs of mature rabbits (the two mature pairs from the previous month plus the baby pair from the previous month, which will have now matured). We note that three new pairs of babies will be born at the end of the month; not counting these new pairs there are now 5 pairs of rabbits.
By now we can note that the number of baby pairs born at the end of month will be equal to the number of mature pairs in that month, and that this number will be the number of baby pairs at the beginning of the next month. This is indicated in the t = 1 row of the table by the red arrow from the 1 in the mature column to the 1 in parentheses in the 'born at the end of the month' column, then to the 1 pair of baby rabbits at the beginning of the second month. Rather than drawing these two arrows we could have just drawn and arrow from the 1 in the mature column in the t = 1 row to the 1 in the baby column of the t = 2 row.
We could do the same for every row of the table, drawing and arrow from the number of mature pairs in one month to the number of baby pairs in the next to indicate that the two numbers are identical.
We also draw an arrow from the 1 in the total column of the t = 1 row to the 1 in the mature column of the t = 2 row, since all the rabbits counted in the total for the t = 1 row will be mature in the subsequent month represented by the t = 2 row.
We can do this for every month, since number of mature rabbits in a given month is equal to the total number of rabbits counted in the previous month.
Proceeding in this manner we obtain the table below.
Now we look at the pattern in the 'total' column. We let a(0) denote the total of the first row, a(1) the total of the second row, etc..
We can see that, starting with the t = 2 row where a(2) = 2, each number is a sum of the two numbers above. For example,
We can see why this scheme works by considering what these numbers mean for any given row. For example, if n = 9, we have a(9) = a(8) + a(7). As indicated in the figure below, a(7) = 21, a(8) = 34 and a(9) = 55.
Looking at the situation from the beginning of the ninth month, we see that two months ago there were a total of 21 pairs of rabbits. We know that sum of these rabbits were babies and some were mature at that time. It doesn't matter how many of each category there were at that time, because it beginning of the eighth month all 21 of these rabbits were mature and ready to reproduce. As a result we have 21 pairs of baby rabbits at the beginning of the ninth month. More generally, we see that the number of babies we have in any month is the number of mature pairs we had in the previous month, which is the total number of pairs we had the month before that.
More generally we see that the number of babies at t = n is equal to the total number of rabbits at t = n-2, or to a(n-2).
From the beginning of the ninth month, we also look back in see that there were 34 pairs alive at the beginning of the eighth month. Since all these pairs survive, we will have in addition to the 21 pairs of baby rabbits, the 34 pairs from the previous month. Sum of these rabbits were babies at beginning of the previous month while some were mature but, since rabbits mature in a month, all 34 of these pairs will now be mature.
More generally we see that the number of mature pairs at t = n is equal to the total number of rabbits at t = n-1, or to a(n-1).
So we see why a(9) = a(8) + a(7). a(8) is the number of rabbits surviving from the previous month, and a(7) is the number of baby rabbits at the beginning of the month.
We see that more generally a(n) = a(n-1) + a(n-2), since at t = n we will have a(n-1) pairs of (now-mature) pairs from the previous month and a(n-2) pairs of babies from the a(n-2) rabbits from two months previous, which have produced babies because they were mature at the beginning of the previous month.
The entire rabbit model is therefore described by the rule at the bottom of the figure above, which states that
Applying this rule for n = 2, then for n=3, then for n=4 we obtain the sequence of totals in the original table. The sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, ... that results from this rule is called the Fibonacci sequence.
We could define a similar sequence, which we call a 'Fibonacci-like' sequence, by the rule given in the figure below. Here we obtain the number in a given month by adding the number from the previous month to double the number from the month before that. If we recall the interpretation of the original Fibonacci sequence, it isn't difficult to see that this rule corresponds to an apparently genetically engineered species of rabbits which never die (so we add the entire a(n-1)), which mature in 1 month (so that the number of baby pairs in month n is equal to the total number of pairs in month n-2), and in which each mature pair produces 2 pairs of baby rabbits at the end of a month.
Our initial conditions for this situation are identical to those of the original model and which we started with 1 pair of baby rabbits and as a result still had just one pair of rabbits at t = 1. Thus we say a(0)= 1 and a(1) = 2.
Without even thinking of rabbits, we can simply follow the rule, knowing that we will obtain the correct numbers and that we can go back and interpret those numbers anytime we wish.
Starting with n = 2, we see that the rule tells us for this value of n that a(2) = a(2-1) + 2 a(2-2) = a(1) + 2 a(0). Since we know a(1) and a(0), we simply substitute their values to obtain a(2) = 1 + 2 * 1 = 3.
Now we can substitute n = 3 to obtain a(3) = a(2) + 2 a(1). Since we just found a(2), we can substitute to get the result a(3) = 3 + 2 * 1 = 5.
For n = 4, we obtain a(4) = 5 + 2 * 3 = 11 and for n = 5, we obtain a(5) = 11 + 2 * 5 = 21.
We now turn to the consideration of how we maintain a certain concentration of an antibiotic in our bodies by taking regular doses of the drug.
Suppose that we take a 500 mg dose every twelve hours, and that in twelve hours we eliminate 70% of the amount of the drug in our body at the beginning of the period.
If we take our first dose at t = 0, then we will have 500 mg of the drug in our body at t = 0. Twelve hours later we will have eliminated 70% of the drug and will therefore have 30% or .3 of the 500 mg, or 150 mg, left. We note that we will have eliminated .7(500 mg) = 350 mg during that period.
We will measure t in the number of twelve-hour periods. Therefore at t = 1, when we take our next 500 mg dose, we will still have 150 mg in our body so that the additional 500 mg gives us a total of 650 mg. At the end of the period we will have .3(650 mg) = 195 mg left and will have eliminated the other 455 mg.
It follows that at t = 2 we will add our 500 mg dose to the 195 mg that still remain, so we will have 695 mg of drug in our body. Of this we will maintain 208 mg and eliminate 487 mg.
If we look at the amount eliminated in each period, we see that the numbers are getting closer and closer to 500. If we think about it, we will see that the amount eliminated can't go over 500 mg , since we are only adding 500 mg during each period. If we eliminate more than we replace, the amount of drug will go down and this clearly will not happen.
If we did reach the point where we were eliminating 500 mg in each period, this would mean that 70% of the amount at the beginning of the period was equal to 500 mg. If we let L stand for the amount of drug in our body at the beginning of a period, we therefore see that we will be eliminating an amount equal to the dose if
.7 L = 500 (condition for eliminating amount equal to the 500 mg in a period).
We easily solve this equation for L to see that if we have L = 500 / .7 = 714 mg at the beginning of a period, we will eliminate 500 mg during the period, leaving 214 mg. Then when we take the next dose we will add 500 mg to get back to the 714 mg, and we will repeat the same cycle with the same numbers again and again until we miss a dose.
We can model the situation with the difference equation a(n) = .3 a(n-1) + 500, which tells us with the amount at the beginning of the nth period is equal to .3, or 30%, of the amount at beginning of the previous period plus the 500 mg those taken at the beginning of the nth period.
We note that according to this model the loss in the nth period will be 70% of the amount at the beginning of the period, or .7 a(n). The maintenance level of the drug is the level at which the amount eliminated equals the dose. That is,
.7 a(n) = 500 mg (condition for amount eliminated equal to the dose).
Solving this we see again that the maintenance level is L = a(n) = 500 mg / .7 = 714 mg.
We note that it is more traditional to refer to the lowest level of the drug as the maintenance level. In this case we would say that the maintenance level is the 214 mg present before the 500 mg dose is taken.
"