Identifying Equations from Basic-Point Graphs for Linear, Quadratic and Exponential Functions

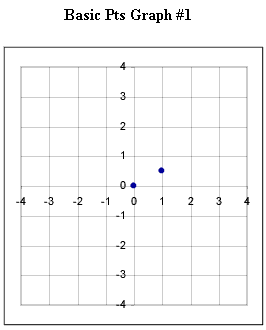
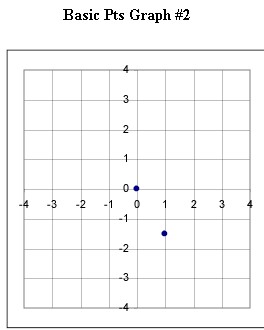
The 17 graphs shown below each depict the basic points for a linear, quadratic or exponential function.  Graphs 1-5 are linear; 6-12 are quadratic and 13-17 are exponential.

You should by now be able to instantly sketch, with reasonable accuracy, the graph of a function if you are given its basic points and the function type (i.e., linear, quadratic, exponential).

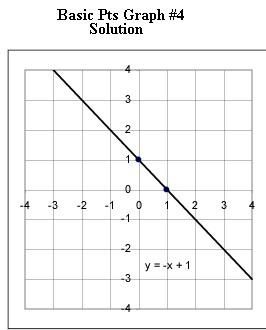
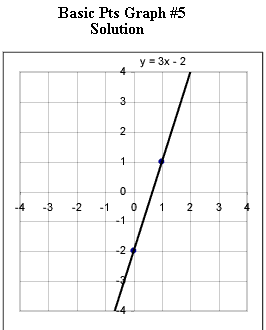
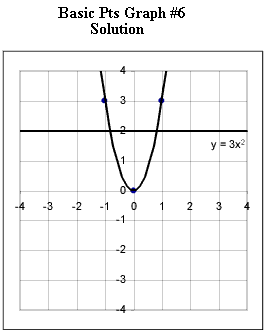
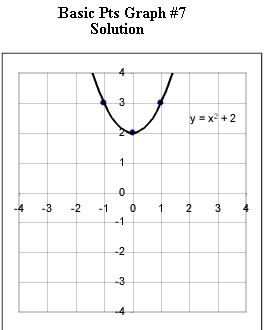
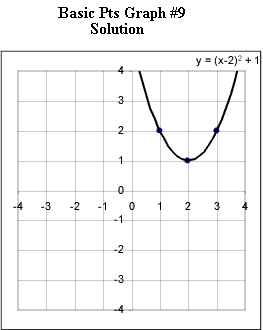
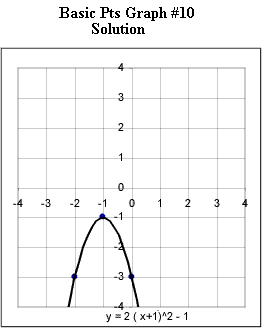
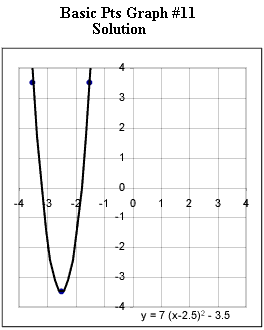
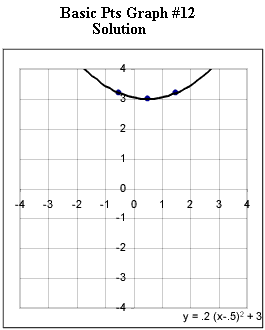
Now you are to determine the equation corresponding to each graph. 

• A linear graph  is represented by the equation y = m x + b, where m is the slope and b is the y-intercept.
• A quadratic graph is represented by the equation y - k = a (x - h)^2, where (h, k) is the vertex and a is the vertical displacement from the vertex to the point lying one unit to its right or left.
• An exponential graph is represented by the equation y = a * b^x + c, where c is the asymptote, a the displacement along the y axis from the asymptote to the first basic point and b the ratio of the vertical the asymptote to the second basic point to the vertical displacement displacement from the asymptote to the first basic point.

Practice until you can instantly identify from the basic points the important characteristic of each graph and determine its equation.

We will continue to refine our understanding of these functions throughout the course.

Graphs            Solutions

Graphs

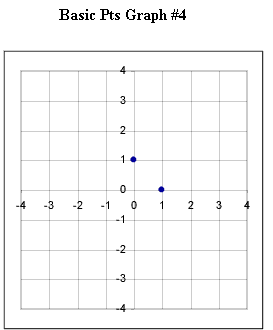
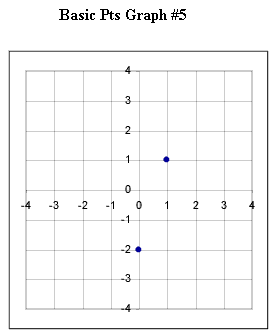
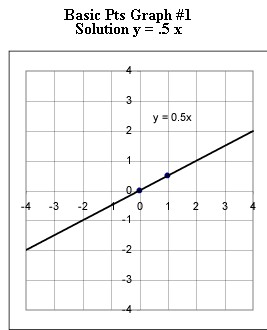
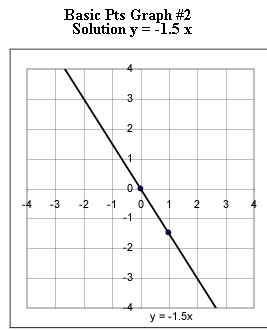
Graphs #1 - # 5 each represent the two basic points for a linear function.  Sketch the graph of the linear function corresponding to each set of basic points.

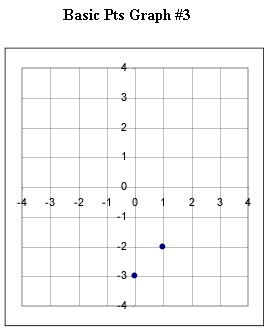
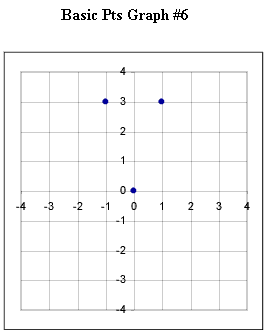
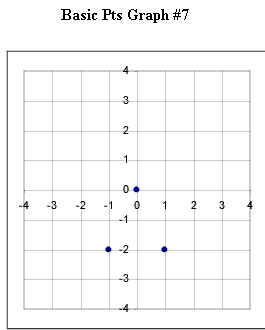
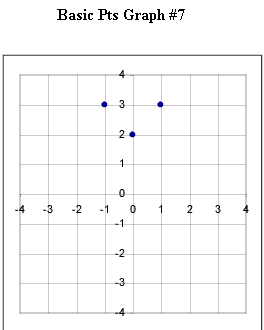
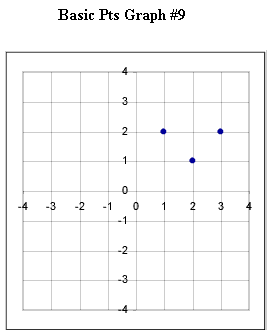
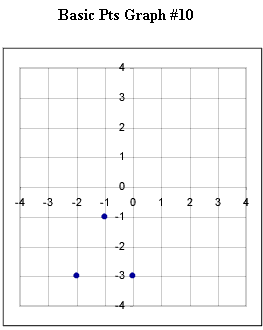
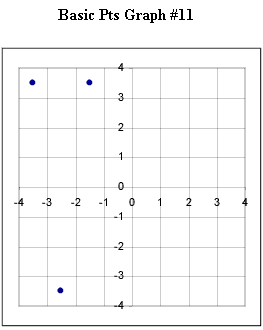
Graphs #6 - # 12 each represent the two basic points for a quadratic function.  Sketch the graph of the quadratic function corresponding to each set of basic points.

Note:  The graph below should be labeled #8.

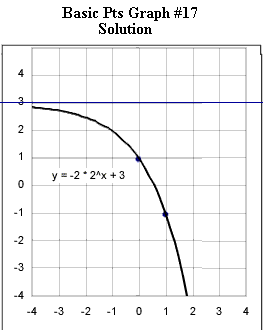
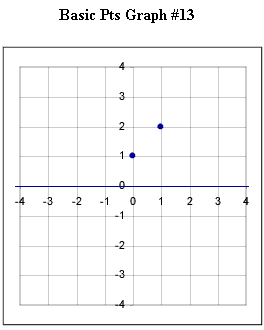
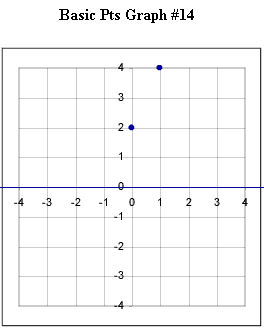
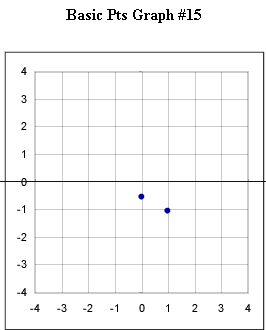
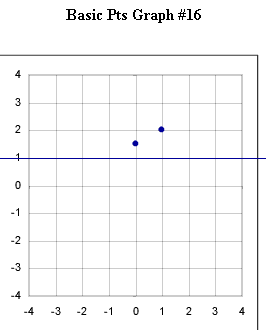
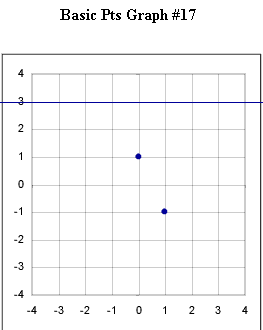
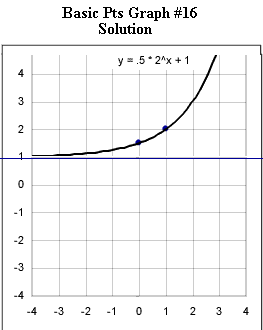
Graphs #13 - # 17 each represent the two basic points for a exponential function with the horizontal asymptotes indicated in the original figure.  Sketch the graph of the exponential function corresponding to each set of basic points.

The horizontal asymptote for graph #13 is the x axis.

The horizontal asymptote for graph #14 is the x axis.

The horizontal asymptote for graph #15 is the x axis.

The horizontal asymptote for graph #16 is the line y = 1.

The horizontal asymptote for graph #17 is the line y = 3.

Solutions

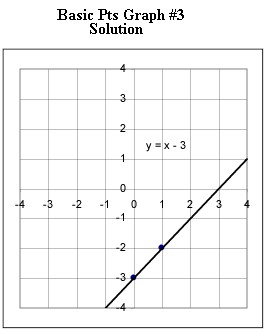
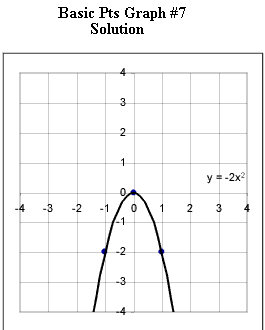
Note:  The graph below should be labeled #8.

The correct function below is y = 7 ( x + 2.5)^2 - 3.5:

Horizontal asymptote is the x axis.

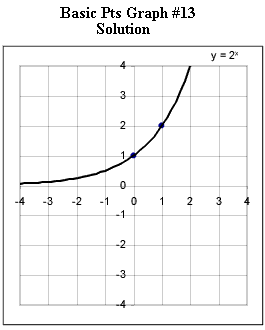
Horizontal asymptote is the x axis.

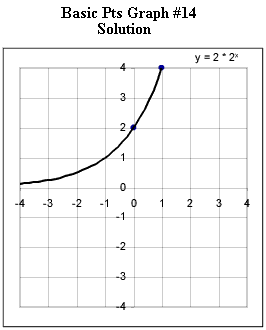
Horizontal asymptote is the x axis.

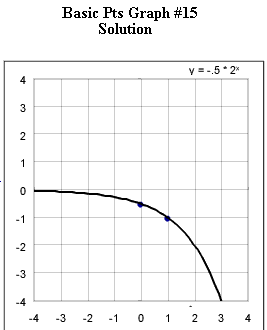
Horizontal asymptote is the line y = 1.

Horizontal asymptote is the line y = 3.