Precalculus II
Class Notes, 1/07/99
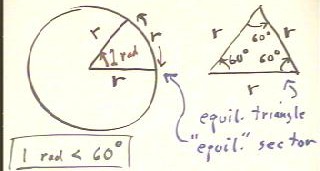
The figure below shows the definition of a radian.
We begin by thinking about an equilateral triangle, as shown at right.
- The three sides of the triangle are equal, and all angles
are equal and therefore 60 degrees (three equal
angles that add up to 180 degrees must each be 60 degrees).
The circle shown that left has radius r.
We construct an 'equilateral sector' of the circle.
- We start at the center and move straight out to the rim of
the circle, a distance r.
We then move a distance r along the arc of the circle.
We finally move straight back to the center.
Each 'side' of this sector has length r equal to the radius
of the circle.
The angle formed at the center of the circle is
defined to be 1 radian.
If we wish to deform an equilateral triangle into an equilateral
sector, we might to bend one side into the arc of
a circle.
- Since the shortest distance between
two points is a straight line, this would bring the two end
points of this side closer together and thereby decrease
the angle between the two sides that remain straight.
- Thus we see that the angle at the center of
equilateral sector has to be slightly less than 60 degrees.
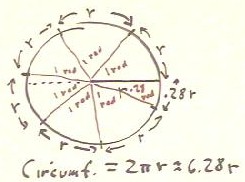
We are interested in determining how many 1 radian sectors are
required to go all the way around a circle.
- We know that each 1 radian sector has an arc length of r,
equal to the radius of the circle.
- We also know that the total arc distance around the circle is its circumference
2 `pi r, or approximately 6.28 r.
- It should therefore be clear that we can fit a little over 6 arcs of
length r around the circle.
- A little more precisely we can fit about 6.28 arcs of length r around
the circle.
- The exact number of arcs of length r that can be fit around a circle is
2 `pi.
We thus say that the angle around a circle is 2 `pi radians.
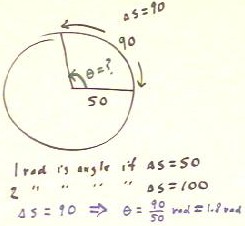
On the circle below we have an arc of length 90 on a circle of radius 50. How many
radians are in the indicated angle `theta?
We can easily reason out the answer to this question.
- If the length of the arc was equal to the radius 50,
then we would have an 'equilateral sector' and the angle would be 1 radian.
- The length of the arc is greater than the radius 50,
so clearly the angle is more than 1 radian.
- An angle of 2 radians would have an arc of length
100, so clearly an arc of length 90 will be associated with
angle less than 2 radians.
- The arc is closer to 100 than to 50, so the angle is closer
to 2 radians than to 1 radian.
- We can find the arc by simple proportionality.
We have 90/50 of the arc necessary for 1 radian, so
the angle must be 90/50 radian = 1.8 radian.
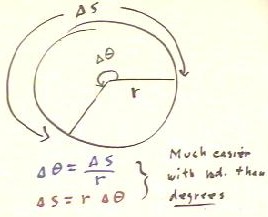
We can symbolize what we just did.
We let `d`theta stand for the angle and `ds for
the arc, and of course we let r stand for the radius.
- We see that in the previous problem the arc was `ds = 90 and
the radius was r = 50. The angle `d`theta was
to be found.
- We divided the arc `ds = 90 by the radius r =
50 to get the angle `d`theta = 1.8 radians.
- We thus see that the angle `d`theta, in radians, is
found by dividing the arc `ds by the radius r.
- Symbolically we can then say that `d`theta = `ds / r.
There are at least two good reasons we use radians
instead of degrees in much of our mathematics:
- While we are used to thinking of angles in
degrees, for calculations involving the arc length on a
circle and the corresponding angle at the center of the circle, the relationship
between arc and angle is much simpler when we measure our angle
in radians.
- When we do calculus with trigonometric
functions, the expressions we have to manipulate are far
simpler when the angles are measured in radians.
It is important to know the angles we get when we divide the
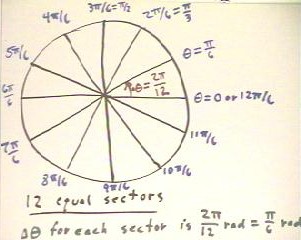
circle into either 8 or 12 equal sectors.
- If we divide a circle into 12 equal sectors, then it is clear that each
sector will contain 360 degrees / 12 = 30 degrees.
- Similarly we see that dividing a circle into 12 equal sectors gives us
sectors each with angle 2 `pi / 12 radians = `pi / 6 radians.
- If we now place the sectors one next to the other around the circle, starting at angular
position 0 on the circle, we obtain angular positions `pi / 6, 2 `pi / 6,
3 `pi / 6, . . . , 12 `pi / 6 radians, as shown below.
- These angular positions can often be reduced to lowest
terms, as indicated in the figure below (e.g., 2 `pi / 6 = `pi / 3; you should
reduce the others similarly, where possible).
- It is essential that you know this picture and that you be able to construct
it on paper within 30 seconds, or mentally construct it almost
instantaneously.
The analogous figure is shown below for a circle divided into 8 equal sectors.
- The angle of each sector is 2 `pi / 8 radians = `pi / 4 radians,
corresponding to a degree measure of 360 deg / 8 = 45 deg.
- You should know how to construct this figure just as quickly as the
other.

