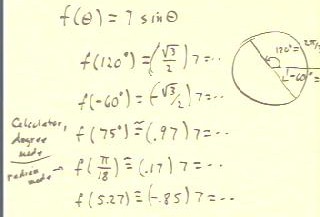Precalculus II
Class Notes, 1/19/99
We develop here the details required for a good understanding of the sine
function. Once you understand the material presented here, the cosine
function can be easily understood through an analogous development.
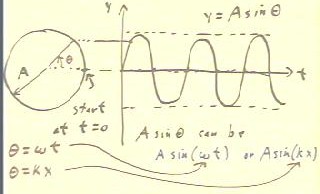
The quantity A sin(`theta) is defined to be the y coordinate of
the point whose angular position, on a circle of radius
A whose center is at the origin of an x-y coordinate system, is `theta,
as measured from the point that intercepts the positive x axis.
The graph we obtain when we plot the y coordinate of this point, with
a circle positioned with its center on the horizontal axis, is therefore the graph of y
= A sin(`theta).
We can interpret this graph as a position vs. clock time graph,
or as a displacement vs. position graph:
- If `theta represents the angular position at clock
time t corresponding to motion with angular velocity `omega,
then `theta = `omega * t and our graph represents y = A
sin(`omega * t) vs. t.
- If `theta = k * x, where x is a position along
a wave and k is a constant (called the wave number),
then our graph could represent y = A sin(k * x) vs. x.
This graph would represent a 'snapshot' of the actual wave.
We can find the exact value of the sine of any
multiple of `pi/6 or `pi/4 from basic geometry,
using the Pythagorean Theorem and very basic facts about
triangles.
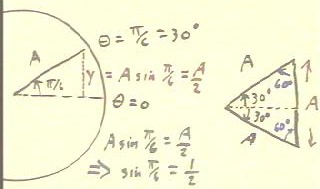
- If we sketch on a circle of radius A the sector whose angle is `pi/6,
as depicted below, we can form the indicated right triangle, with y
as the side opposite the angle.
- We are familiar with the fact that `pi / 6 = 30 degrees. For a moment
it will be simpler to work in degrees.
- If we place two copies of this right triangle with as
shown below, we form an equilateral triangle whose sides are
A.
- It should be clear from this figure that y = A / 2.
- Since y = A sin(`pi / 6), we have A sin(`pi/6) = A / 2. We can solve
this equation to obtain sin(`pi / 6) = 1/2.
We can also find the sine of `pi/4, or 45 deg, by looking at the triangle
formed as indicated in the figure below.
- From the symmetry of the triangle we can see that the two shorter sides of
the triangle are equal. We call the length of the sides s.
- From the Pythagorean Theorem we therefore see that A^2 = s^2 + s^2.
- Solving this equation for s, as indicated below, we
see that s = 1 / `sqrt(2) * A.
- Setting y = A sin(`pi / 4) = s = 1/`sqrt(2) * A, we
have an equation that we can solve for sin(`pi/4).
- Solving the equation we see that sin(`pi/4) = 1/`sqrt(2) = `sqrt(2) / 2.

The approximate values of `sqrt(2) / 2 and `sqrt(3) / 2 are .71 and
.87.
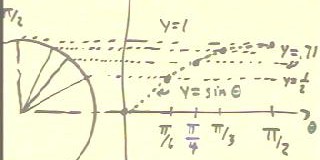
- We therefore obtain the table depicted in the figure below for the approximate
values of y = sin(`theta).
- The circle at right depicts angles of 0, `pi/6, `pi/4, `pi/3
and `pi on a circle of radius 1.
As you can see we are the projecting the y coordinates of
these points to a graph of y vs. theta.
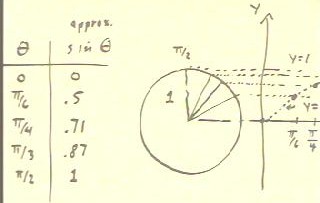
The graph is shown below in some detail. The dotted lines are
y = 1/2, y = .71, y = .87 and y = 1.
- We note that `pi/6, `pi/3 and `pi/2 are equally spaced, dividing the interval
from 0 to `pi/2 into 3 equal segments (not
shown too accurately on the figure below; you should be able to do better).
- `pi/4 cuts the interval from 0 to `pi/2 in
half, as depicted below; `pi/4 also lies halfway between
`pi/6 and `pi/3.
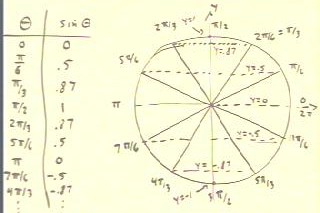
We can extend our table past `pi/2 to encompass
angular positions around the entire circle (and beyond, into a second or
third cycle, actually into any number of cycles, if we wish).
- The table below lists values of sin(`theta) vs. `theta for
multiples of `theta = `pi/6, up through the
third-quadrant angle 4 `pi / 3.
- The table is made with the aid of the circle depicted at right.
- The symmetry of the situation dictates the indicated y
coordinates on the circle, in an obvious way.
- You should be able to produce this table and this picture
instantly anytime you need it.
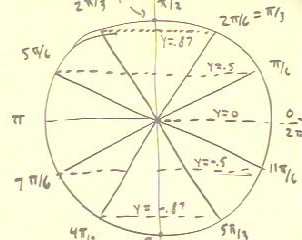
The figure below depicts the circle a bit more clearly.
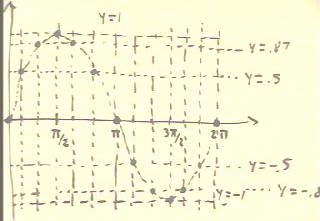
In the next figure the horizontal dotted lines depict the y
values corresponding to multiples of `pi/6.
- The vertical dotted lines divide the cycle from 0 to `pi/2 into
12 equal intervals, corresponding to the multiples of `pi/6.
- You should be able to produce this graph instantly anytime you need it.
To evaluate the function f(`theta) = 7 sin(`theta), we can use exact values of the
sines of angles which are multiples of `pi/6 (30 deg) or `pi/4 (45 deg) whenever we have
those angles. Otherwise we can use a calculator, being careful to use the degree or radian
mode where appropriate, to find the sines.