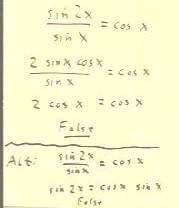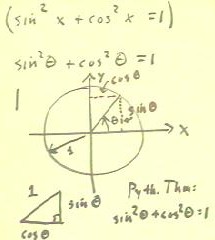Precalculus II
Class Notes, 1/26/99
Trigonometric Identities
The first of the essential
trigonometric identities is the Pythagorean identity, expressed in your
text as sin^2(x) + cos^2(x) = 1.
- Here we will express the identity in terms of the circular model and
use `theta rather than x for the variable.
In this case the identity becomes sin^2(`theta) + cos^2(`theta) = 1, as
depicted in the second line below.
- The circle in the figure has radius 1, so the sine and
cosine of `theta are the x and y coordinates of
the point on the circle corresponding to angle `theta.
- It should be clear that the sine and cosine of `theta
therefore correspond to the lengths of the two projection
lines,as labeled below.
- It should also be clear that the sine and cosine are
the legs of the right triangle depicted at the bottom of
the figure.
- Applying the Pythagorean Theorem to the triangle we
obtain sin^2(`theta) + cos^2(`theta) = 1.
- Note that this identity can easily be changed to read sin^2(`theta) = 1 -
cos^2(`theta), or to cos^2(`theta) = 1 - sin^2(`theta).
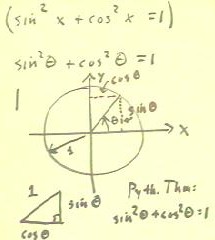
Reflection Identities
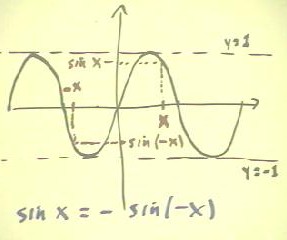
The graph below depicts y
= sin(x).
We note that for any x there is a -x on the opposite
side of the y axis, and that the y coordinate at
-x is the negative of the y coordinate at
x.
We similarly note that for a graph of y = cos(x), the
value of the function at -x is the same is
that at x, as indicated in the figure below.
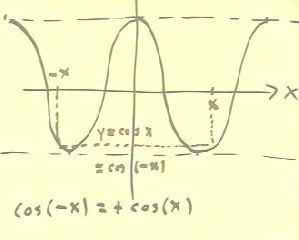
Formulas for Sum of Two Angles
By either geometric or analytical means we can derive
the identities for the sine and cosine of
the sum of two angles a and b.
The formulas for sin(a + b) and cos(a + b) are given
at the top of the figure below.
From these formulas we can draw a number of useful
and interesting conclusions:
- In the third line we see that sin(2x) = sin(x + x).
- substituting a = x and b = x into the identity for sin(a
+ b) we obtain the indicated expression.
- We easily simplify this expression to show that sin(2x) = 2
sin(x) cos(x).
- At the bottom of the figure we apply a similar procedure to
show that cos(2x) = cos^2(x) - sin^2(x).
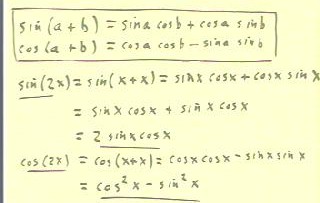
We can apply the reflection identities to obtain the expressions for
the sin or cosine of the difference of
two angles:
- We substitute a = x and b = -y into the identity for sin(a+b)
to obtain the expression the first line of the figure below.
- We then recall the reflection identities cos(-y) = cos(y) and sin(-y) =
- sin(y) to simplify this expression and see that sin(x-y) = sin
x cos y - cos x sin y.
- We follow a similar procedure for cos(x-y), obtaining
the formula indicated below.
- We can summarize the formulas for the sum or difference
of two angles as indicated in the last two lines of
the figure.
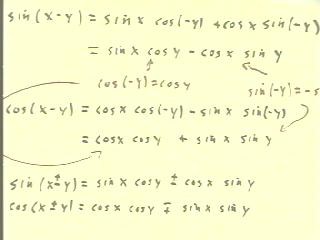
We can also use the Pythagorean identity to change the form of the
formula for cos(2x), obtaining two different forms as indicated below.
- In both cases we start with the identity cos(2x) = cos^2(x) =
sin^2(x).
Substituting 1 - sin^2(x) for cos^2(x) we obtain the
first formula, cos(2x) = 1 - 2 sin^2(x).
Substituting 1 - cos^2(x) for sin^2(x) we obtain the
second formula, sin(2x) = 2 cos^2(x) - 1.
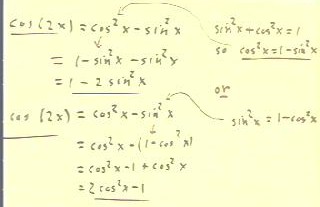
We also have the Law of Cosines, written in the first line of
the figure below.
- For the right triangle shown in the figure, the Pythagorean
Theorem tells us that c^2 = a^2 + b^2.
- The Law of Cosines tells us that c^2 = a^2 + b^2 + 2 a b
cos(C).
- It appears that the two laws are telling us two different
things about the same triangle.
- However, for a right triangle, C = 90 deg, so that cos(C)
= 0 and the two expressions turn out to be identical.
- If we do not have a right triangle, then the
expression -2 a b cos(C) can be regarded as a 'correction' of
the Pythagorean Theorem, compensating for the fact that we do not have a right
triangle.

Proving Identities
Consider the equation shown
below, sin(2x) / sin(x) = cos(x).
If this equation is true for all x, then we call it an identity.
We might be able to determine whether the equation is an identity
by substituting 2 sin(x) cos(x), from the double-angle
identity, for sin(2x).
- When we do so we obtain an equation which quickly reduces to 2
cos(x) = cos(x), which we know not to be true for at least some values of x
(e.g., it is false if x = 0, since 2 does not equal 1).
- Since the equation is not always true, it is not an identity.
- Another approach might be to multiply both sides of the equation by the
denominator sin(x), as shown that the bottom of the figure below.
- We obtain sin(2x) = sin(x) cos(x), which contradicts the
known identity sin(2x) = 2 sin(x) cos(x).