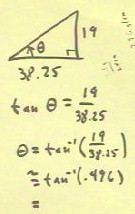Precalculus II

Class Notes, 1/28/99

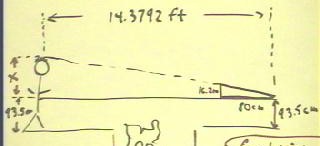
James is 14.3742 feet away, across a chasm protected by a red-eyed ogre.  We want to know how tall Janes is.

• We know that the ground on both sides of the chasm is level and at the same height.
• We sight along a level table 93.5 cm high, and along a string lined up with James' head, as shown.
• We measure the rise of the string for a run of 80 cm, and find that the rise is 16.2 cm.

We want to use these results to determine James' height.

The triangle formed by the string and the tabletop is similar to the larger triangle formed by the lines of sight along the string and the tabletop, and by James' height from table level to top of head.

• The ratio of rise to run for the small triangle is 16.2 / 80 = .2025.
• The ratio of James' height x from tabletop to headtop to the 14.38 ft. distance must therefore also be .2025.
• Thus the distance x must be .2025 * 14.38 ft = 2.91 ft.
• James' height must therefore be the 93.5 cm = 37-inch height of the tabletop plus the 2.91 ft. = 34.9" height, or 71.9".
• James reports being 5' 11.5" tall; with shoes he should be nearly half an inch taller.
• The agreement is excellent.

The similarity of the triangles could be expressed as rise1 / run1 = rise2 / run2.

• If triangle 1 has rise x and run 14.38, and triangle 2 has rise 16.2 and run 80, then by setting the ratios equal we get the equation in the figure below.
• Solving the equation we get x = 2.91 ft., as before.

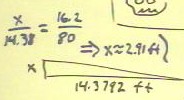
Measurement of the height of the flagpole in front of VHCC used the parameters indicated in the figure below.

• A level sighting was taken from a height of 49 inches.
• A sighting to the top of the pole was characterized by a line whose slope was indicated by a rise of 19" and a run of 38.25".
• The horizontal distance from the point of sighting to the base of the pole was found to be 63 feet.
• The distance x from the level of the sighting to the top of the pole, indicated in the figure, is therefore found from the similarity of the triangles (setting rise/run ratios equal) to be 31 feet.
• The same distance is easily found be multiplying the 63' distance by the 19" / 38.25" = .496 ratio of rise to run.
• The height of the pole is therefore 31' + 49", or very nearly 35 feet.

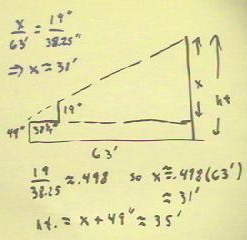
The ratio of the rise to the run is called the tangent of the angle `theta, where `theta is the angle opposite to the rise.

• The tangent of `theta for the flagpole is therefore 19/38.25 = .496.
• Using the inverse tangent (2d fn or inverse, then tan on your calculator) we can find the angle `theta.