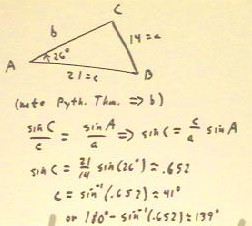Precalculus II
Class Notes, 2/02/99
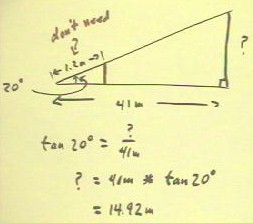
To determine the height of a flagpole from the 20
degree angle of the line of sight with a horizontal line
to the base of the flagpole, given the horizontal
distance to the base of the flagpole, we write the definition of
the tangent of this angle for the given situation.
- We obtain the equation indicated below, which we solve to
find that the height of the flagpole is 14.92 meters.
- Note that the 1.2 m distance indicated on the figure is unnecessary
if we know the angle.
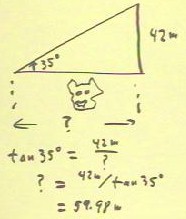
To determine the distance to a tree whose known
height is 42 meters, across a chasm protected by a
red-eyed ogre, we need only know the angle of inclination of
our line of sight to the top of the tree with respect to
a horizontal line of sight to its base.
- If the angle is 35 degrees, then the definition
of the tangent is as indicated.
- We easily solve this equation for the unknown distance,
which is 59.98 m.
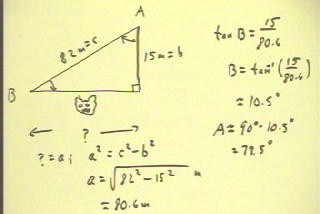
If in a similar situation we know the distance to the top of the tree
from a point at the same level as the base, we
can easily determine the angle of the line of sight as
well as the horizontal distance to the base of the tree.
- As indicated below, we use the Pythagorean Theorem to obtain the horizontal
distance to the base.
- We can then use this horizontal distance and the height of the tree to
write the definition of the tangent, which we solve to
find that the desired angle is 10.5 degrees.
- The other angle of our triangle is easily found to be 78.5
degrees.
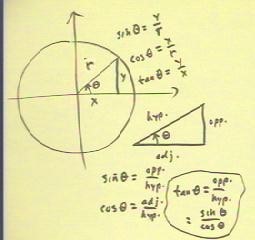
Recall the circular definitions of the sine, cosine and
tangent of an angle.
- The definitions used for triangles
use the labels 'opposite', 'adjacent' and 'hypotenuse' to
indicate the three sides of the triangle relative to the
angle `theta.
- In terms of these labels we have
the definitions shown that the bottom of the figure below.
- It should be clear that these
definitions are completely equivalent to the circular definitions.
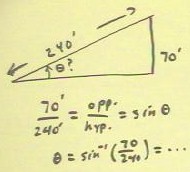
For the triangle indicated below, we see that the definition of the sine
of an angle as the opposite side over the hypotenuse tells
us that the sine of `theta is 70 / 240,
from which we can easily determine the angle, as
indicated.
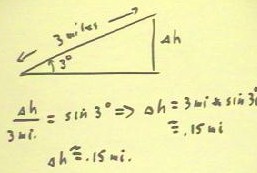
If we walk 3 miles up a hill which is inclined at 3
degrees with horizontal, the associated altitude change
`dh is easily found.
- We see that `dh / 3 miles must be equal to the sine
of 3 degrees.
- Writing this relationship as an equation we easily solve for
`dh, as indicated.
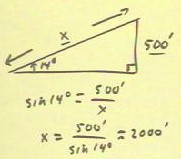
If we wish to find the distance we must travel along a 14
degree incline in order to change our elevation by 500
feet, we construct the triangle indicated
below.
- We write the definition of the sine of 14 degrees and solve
for the unknown hypotenuse x.
The Law of Sines and the Law of Cosines are stated in
the figure below.
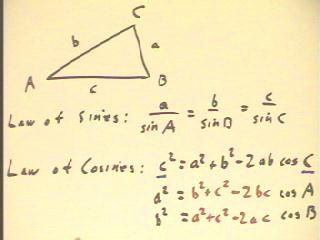
As an illustration we use these laws to determine the unknown
sides and angles of the triangle below.
- It would be possible to use the Law of Cosines to find the length of
the side b: the equation a^2 = b^2 + c^2 - 2 b c cos(A) would
have only the side b unknown. However, this equation is quadratic
in b and it is more convenient to find the simpler
means of solution, and hopefully one that gives a single
result.
- If we use of Law of Sines as indicated we can determine the angle
C, or more correctly, the two possible angles C.
- There are two solutions between 0 and 180 deg to the equation sin
C = .652, one <90 degrees and one > 90 degrees.
- We would have to use information about the specific situation to
determine which of the two solutions is appropriate
to the situation.
- Having determined which angle is appropriate, we then can determine the
third angle of the triangle from the fact that the angle add up to 180
degrees.
- We could then find the side b using the Law of Cosines.