Precalculus II
Class Notes, 2/04/99
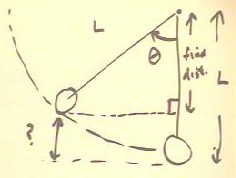
When a pendululm of length L is displaced
to angle `theta from its vertical equilibrium position,
how high is it above its low point?
- A horizontal line from
the position of the pendulum to the vertical
line at the equilibrium position will form the indicated
right triangle.
- If we can find the vertical
side of this right triangle, we can subtract it from the length
L of the pendulum to find the desired height.
- We easily see that the desired
leg of the triangle has length L cos(`theta).
- The height is
therefore L - L cos(`theta) = L ( 1 - cos(`theta) ).
If we displace a pendulum of length 118 cm a
distance of 30 cm from its equilibrium position, then
since the angle `theta is fairly small we can say that `theta
= tan^-1 (30 / 118) = 14.2 degrees, approximately.
- In this case, the previous result tells us that the pendulum should
be 3.6 cm higher than its low point.
- Measurements made on an actual pendulum with these
dimensions in this displacement indicate a difference of
3.7 cm in altitude, which is well within experimental error
of the prediction.
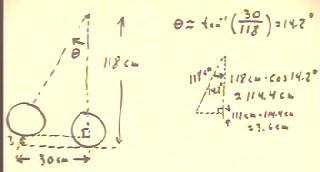
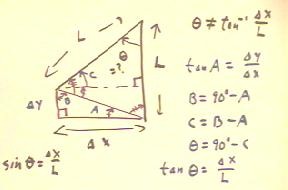
The use of the tangent function for the pendulum situation was
not completely correct. If we sketch the figure with a larger
displacement and hence a larger angle `theta, we see that `dx
is not actually the opposite side of a right
triangle with adjacent side L.
- We could try to patch up the difference using the angles A, B
and C indicated in the figure below. We would end up with something like three
simultaneous equations in three unknowns, which we could solve
to find `theta. The appropriate equations are
indicated on the right-hand side of the figure.
- It would, however, be much easier if we simply noted that sin
(`theta) = `dx / L and used the inverse sine rather than the inverse
tangent to find `theta.
- Alternatively we could use the Pythagorean Theorem to find the vertical
side of the right triangle, and avoid the use
of sines and tangents altogether.
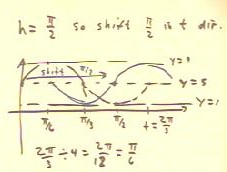
In order to graph the function indicated in the
figure below, we note that the function is of the form y = A sin(`omega ( t - h) )
+ c.
- We sketch the circular model for A = 4, `omega = 3 and c = 5.
- The reference circle will have radius 4 and will be centered
at y = 5.
- The period will be T = 2 `pi / `omega = 2 `pi / 3, so
the cycle will be completed between t = 0 and t
= 2 `pi / 3.
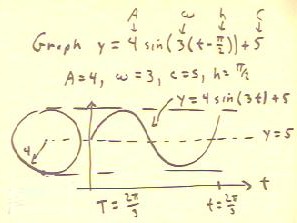
To graph the function as given we must take account of the horizontal shift h =
`pi / 2.
- To help sketch the graph accurately we divide the period 2 `pi
/ 3 into four equal segments of length (2 `pi /
3 ) / 4 = `pi / 6.
- We shift the graph `pi / 2 units to the right,
as indicated below.
- The 'blue' graph will be the graph of the given function.