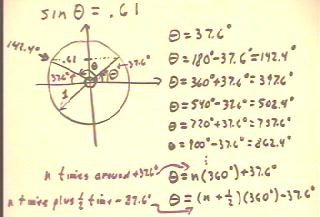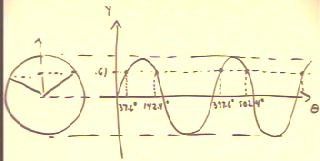
A solution to the equation sin(`theta) = .61 is sin^-1(`theta) = 37.6 deg (approx).

This solution can be represented by sketching a reference circle of radius 1 and determining the angle at which the corresponding y coordinate is .61, as shown below.

• This is pretty simple.  But it turns out that there are infinitely many angles which satisfy the equation sin(`theta) = .61.
• There is also a second-quadrant angle for which the sine is .61. As shown in the figure below this angle lies at 37.6 deg above the negative x axis and is hence 180 deg - 37.6 deg = 142.4 deg.
• It is also possible to start at the positive x axis, pass through the 37.6 deg and 162.4 deg angles, complete a cycle around the circle and end up back at the first-quadrant position where sin(`theta) = .61. In doing so we would have gone through an angle of 360 deg + 37.6 deg = 397.6 deg.
• We could continue from this position to the second-quadrant position for sin (`theta) = .61. In doing so we would go through angle 360 deg + 142.4 deg = 502.4 deg, which can also be expressed as 360 deg + 180 deg - 37.6 deg = 540 deg - 37.6 deg = 502.4 deg.
• We could continue around the circle, arriving again at the first-quadrant angle, after having gone through 720 deg + 37.6 deg = 757.6 deg.
• Continuing around to the second-quadrant angle we would end up at 720 deg + 180 deg - 37.6 deg = 900 deg - 37.6 deg.

In general if we first go n times around the circle, we will go through angle n ( 360 deg), then through 37.6 deg to end up at the first-quadrant angle; we could then continue through another 180 deg = 1/2 (360 deg) and then back 37.6 deg to end up at the second-quadrant angle.

• Formulas for the angles at which we end up after going n times around the circle would thus be

• `theta = n ( 360 deg) + 37.6 deg or
• `theta = (n+1/2) (360 deg) - 37.6 deg.

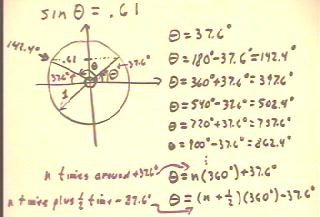
The solutions to the equation sin(3x - 2) = .61 are those values of x for which 3x - 2 is one of the angles found in the preceding figure.

• We can set 3x - 2 equal to each angle in turn and solve each resulting equation for x. This works fine if we only need a few solutions.
• If we want a general set of solutions we set 3x - 2 equal to the general expressions for the angles, as indicated on the right-hand side of the figure below.

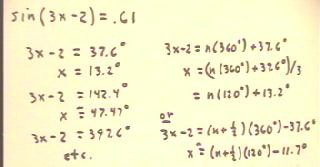
A graph of sin(`theta) vs. `theta is depicted below, with those angles indicated for which the sine is .61.

• This graph shows how the two values found in the first cycle will repeat for subsequent cycles.

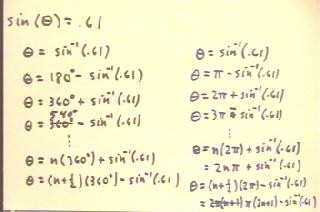
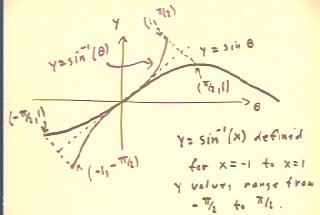
We see below how the graph of the inverse sine function is obtained by inverting the portion of the graph of the sine between - `pi / 2 and `pi / 2.

• The resulting inverse function is defined between x = -1 and x = 1, with y values ranging from - `pi/2 to `pi / 2.
• We choose to invert the sine function over the interval from -`pi/2 to `pi/2 because the function is single-valued over this interval, and over this interval it takes all of its values.

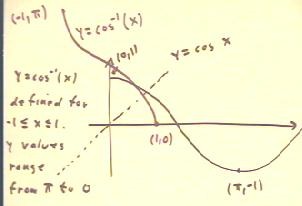
We invert the cosine function from x = 0 to x = `pi, since over their region the function takes each of its values exactly once, so that the inverse function is single valued.

• The resulting inverse function is defined for -1 < x < 1, and takes y values ranging from `pi to 0.