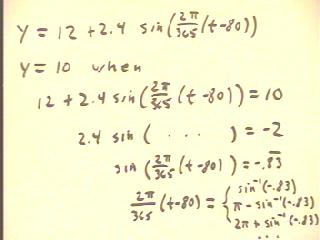Precalculus II
Class Notes, 2/11/99
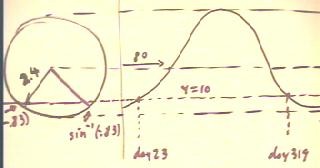
In a certain city, the length of the daylight runs
from 9.6 hours to 14.4 hours on an annual cycle.
- The circular model for y = day length is therefore y
= A sin( `omega (t - h) ) + C, with A = 2.4 and C = 12.
- Since the period of the day-length cycle is 365 days, `omega =
2 `pi / 365.
- The day-length cycle is shifted to the right by 80
days so that we have an increasing 12-hour day length on the 80th
day of the year, so h = 80.
- The result is the model given the figure below.
We wish to determine when the day length is 10 hours.
- We set y = day length = 10 and solve the
resulting equation.
- After doing some simple algebra we arrive at sin( 2 `pi / 365 (t - 80 ) ) =
-.833....
- We write down the solutions using the inverse sine function,
as indicated in the last line.
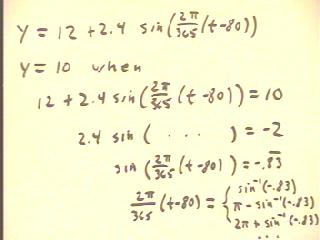
The two solutions that yield t between 0 and
365 days are shown below.
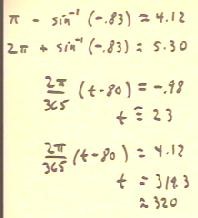
The figure below depicts the circular model and the graph of y
vs. t, showing the positions on the reference circle and
on the graph where y = day length = 10.
- The reference circle, of radius 2.4, is centered
at y = 12.
- The graph is shifted 80 units to the right,
with its midpoint y value occurring at t = 80, where y
is increasing.
The graph below depicts fullness vs. clock time t for 1 cycle of
the moon, with time duration 28 days and hence `omega = 2 `pi / 28.
- The fullness y of the moon goes from 0% to 100%,
so the reference circle is centered at y = 50 and
has radius 50.
- If we wish to determine for how long the moon is at least 99%
full.
- We therefore set y = 99 and solve the resulting
equation, as indicated.
- Our solution indicates that y = 99 at t = 6.1 days
and at t = 7.9 days during the cycle, so that the moon remains at
least 99% full for 1.8 days.
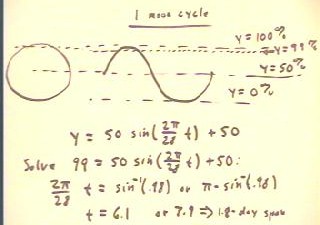
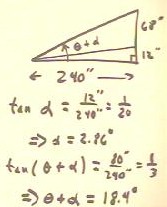
An observer 20 feet from an actor on the stage wishes to determine how
much of her field of vision is filled by the
glorious sight.
- The actor, as indicated, is 68 inches tall and the eye
level of the observer is 12 inches below the feet
of the actor.
- The angles of the observer's line of sight to the feet
and to the head of the actor, measured with
respect to the horizontal direction, are the angles `theta and
`alpha indicated in the figure below.
- `theta is the angle that determines how much of the
observer's field of vision is occupied by the actor.
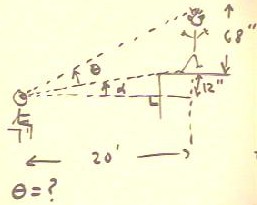
The right triangle below shows that the total angle `theta +
`alpha between horizontal and the observer's line of
sight to the top of the actor's head is tan^-1
(80 / 240) = 18.4 deg, while the angle between horizontal
and the line of sight to the actor's feet is `alpha =
tan^-1(12 / 240) = 2.9 deg.
- The desired angle `theta is therefore easily found by subtracting
`alpha from `theta + `alpha.