Precalculus II
Class Notes, 2/16/99
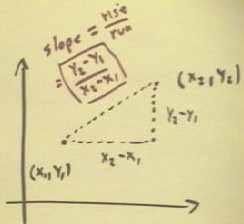
The distance from (x1, y1) to (x2, y2) is found by
applying the Pythagorean Theorem to the fundamental triangle.
- The distance between the points is the hypotenuse of
the triangle.
- The legs of the triangle are x2 - x1 and y2 - y1.
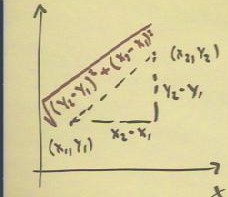
It follows that the distance is as indicated in red below.
The midpoint between (3, 7) and (17, 13) will
have x coordinate halfway between 3 and 17 and
y coordinate halfway between 7 and 13.
- The x coordinate will therefore be (3+17) / 2 and the y
coordinate will be (7 + 13) / 2, as indicated below.
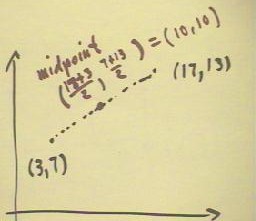
The midpoint can also be found using similar triangles as
in the figure below.
- The x coordinate of the midpoint will be x1 +
1/2 (x2 - x1) = (x1 + x2) / 2, and the y coordinate will be y1
+ 1/2 (y2 - y1) = (y1 + y2) / 2.
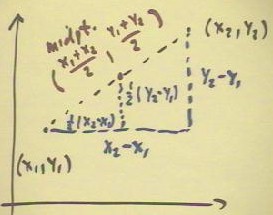
We now consider the problem of finding an equation for the set
of points (x,y) that are equidistant from the points (3
, 10) and (8, 2).
- The distances are as indicated in red in the figure below.
- We set these distances equal and square both sides of the equation.
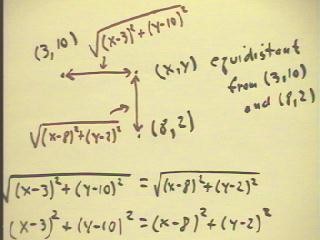
In the third line below we expand the squares.
- In the fourth line we see that the squared terms x^2 and
y^2 disappear when subtracted from both sides, leaving us a linear
equation.
- We solve the linear equation for y to
obtain the slope-intercept form y = 5/8 x + 41/16.
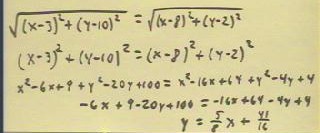
We note that the slope between the two points is -8/5,
while the slope of the straight line we just obtained
was 5/8.
- These slopes are negative reciprocals of one another, showing us that
the line we found is perpendicular to the segment
between the points.
- Since the set of points equidistant from the two points is the perpendicular
bisector of the segment between the points, this confirms at
least the slope of our resulting equation.

We now find a formula for the condition that the sum of
the distances from (-3, 0) and from (3,0) to
point (x,y) is 7.
- The two distances d1 and d2 are as indicated in the
figure below.
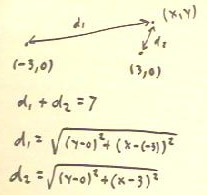
Setting the sum of these distances equal to 7, we
obtain the equation in the second line below.
- We wish to express this equation without the square roots. We will
therefore square both sides of the equation.
- Using the fact that (a + b) ^ 2 = a^2 + 2 a b + b^2, we square
both sides of the equation.
- Somewhat inconveniently, we see that the 2 a b term still leaves us
with square roots. So it might seem like we haven't made any progress
toward getting rid of the square roots.
- However, if as in the second-to-last line below we isolate the square
root factors on the left side, and then simplify the
right side, we obtain an equation we can again
square; this time the square roots will disappear, though we will get some
fourth-power terms (which we hope will cancel out).
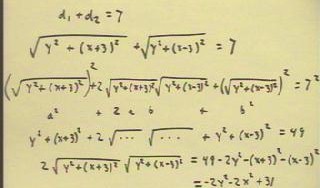
Taking care to square the trinomial on the right-hand
side carefully, we obtain the equation in the second line below.
- We expand the expression on the left-hand side and
note that all fourth-order terms are identical on both
sides and hence can be subtracted out of the equation.
- We are left with the equation 196 y^2 + 52 x^2 = 637, which for reasons
that will become apparent later we express in the form y^2 / b^2 + x^2 / a^2 = 1.
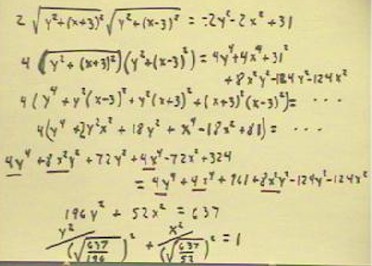
The condition that the sum of the distances from two points to (x,y) is
constant is the condition for an ellipse. So the equation we have
obtained is the equation of an ellipse.
More generally, the equation of an ellipse is, as indicated above, x^2 /
a^2 + y^2 / b^2 = 1.
