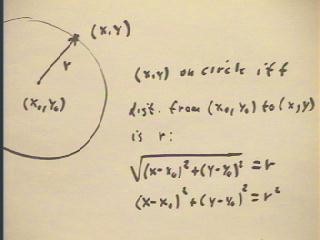Precalculus II
Class Notes, 2/23/99
A point (x, y) lies on the circle of radius r through the (x0, y0) if, and only if, (x,
y) lies at distance r from (x0, y0). This is the definition of a circle of radius r.
- This circle is depicted and the above condition is translated into an equation in the
figure below.
- Squaring both sides of the equation gives us the form (x - x0) ^ 2 + (y - y0) ^
2 = r^2 for the above condition.
- We therefore call this equation the equation of the circle.
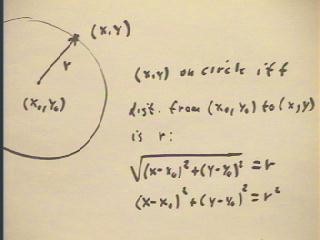
The question was posed of how to find the equation of a circle with diameter
from (2,4) and (10,4).
- Since the center of the circle is the midpoint of any diameter, we
conclude that the center is (6,4).
- Since the distance from (6,4) to either of the endpoints of the diameter is easily found
to be r = 4, we easily find the equation of the circle as depicted below.
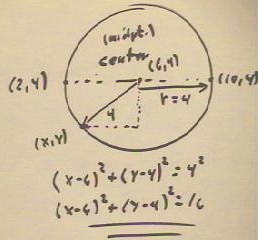
Video Clip #01
Alternatively, we can find the equation of this circle from the fact that any
triangle inscribed in the circle whose hypotenuse is a diagonal must be a right triangle.
- If (x, y) is a point on the circle, then we can inscribe a right triangle with its
right-angle vertex at (x, y) and its hypotenuse on the given diagonal.
- We easily represent the slopes of the line segments from the to endpoints of the
diagonal to (x, y), as indicated below.
- Since these segments are at right angles, these slopes must be negative
reciprocals.
- Setting one slope equal to the negative reciprocal of the other results in the equation
that the bottom of the figure below.
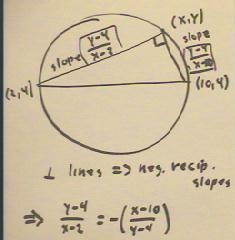
As shown in the figure below, we can rearrange this equation into the standard
form for the equation of a circle.
- In the second line we multiply both sides by the common denominator.
- In the third and forth lines we expand the right-hand side then subtracted from both
sides.
- In the fifth and six lines we complete the square on the x terms.

Video Clip #02
In the last class we found the midpoint between two points by simply
averaging the x and the y coordinates of these points.
- Alternatively we could have used the fundamental triangle indicated in the figure below.
- The sides of the fundamental triangle are (y2 - y1) and (x2 - x1), so the sides of the
smaller fundamental triangle that reaches the midpoint will be half as great.

A close-up of this triangle shows how, starting at (x1, y1) and moving (x2 - x1) / 2
and (y2 - y1) / 2 units in the x and y directions we end up at the indicated midpoint.

This approach is a bit more complicated than simply averaging the coordinates of the
points, but it has the advantage that it generalize is.
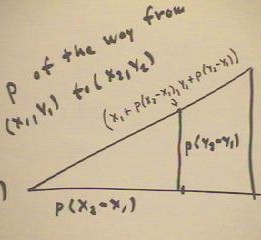
- In the figure below we find the coordinates of the point lying a proportion p of the way
between (x1, y1) and (x2, y2).
- We move thru displacements p(x2 -x 1) and p(y2 - y1) in the x and y directions
respectively, ending up at the indicated point.
Video Clip #03
The equation of a circle of radius r centered at the origin is x^2 + y^2 = r^2.
- We could divide both sides by r^2 and write this equation as x^2 / r^2 + y^2 / r^2 = 1.
- We note that the square of the radius of the circle appears as a denominator under x^2
and under y^2; the right-hand side is 1.

If we wanted a different 'radius' in the x direction than in the y direction we could
use different numbers for the denominators.
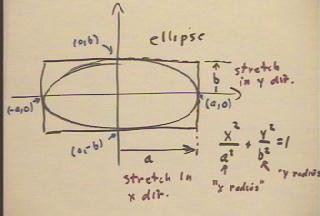
- We might thus interpret x^2 / a^2 + y^2 / b^2 = 1 as a 'deformed circle' with
'radius' a in the x direction and 'radius' b in the y direction.
- We sketch such a shape in the figure below:
- We begin by constructing a rectangle centered at the origin, stretching it in the x
direction so that it reaches the points (a, 0) and (-a, 0), and in the y direction so that
reaches the points (0, b) and (0, -b).
- We then sketch our 'deformed circle' inside this rectangle.
- The resulting shape is an ellipse.
We note that the equation tells us that if y = 0, x = +- a, confirming that the points
(a, 0) and (-a, 0) both lie on the ellipse.
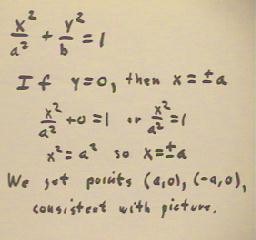
We note that similarly if x = 0, y = +- b, confirming the points (0, b) and (0, -b).
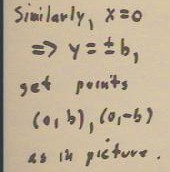
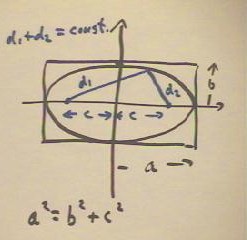
We recall that an ellipse is defined as a set of points such that the sum of the
distances d1 and d2 from two foci is constant.
- For the given ellipse, which is centered at the origin, if the x coordinate of the
ellipse is c, then a^2 = b^2 + c^2, so c = `sqrt(a^2 - b^2).
- If b > a, then the foci lie on the y axis at distances c from the origin and b^2 =
a^2 + c^2, so c = `sqrt(b^2 - a^2).
Video Clip #04
In class we constructed an ellipse on the floor by holding a somewhat slack length of
string on the floor at points approximately 2.35 ft apart.
- The resulting distances from the center of the ellipse to the extreme points were 2.55
ft in the x direction and 1.2 ft in the y direction.
- The resulting values of a, b and c are reasonably consistent with the condition a^2 =
b^2 + c^2.
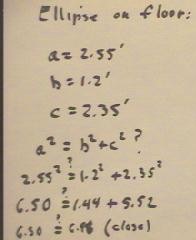
Video Clip #05
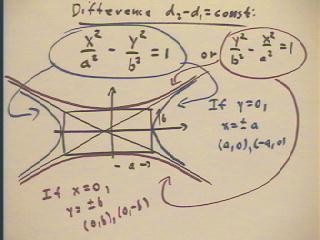
If we set the difference d2 - d1 of the distances to two foci (at
equal distances from the origin in the x direction) equal to a constant,
we will obtain an equation which reduces to x^2 / a^2 - y^2 / b^2 = 1.
If the two foci are at equal distances from the origin along the y axis, we
will obtain the equation y^2 / b^2 - x^2 / a^2 = 1.
- The figures corresponding to these equations can be constructed by first constructing
the same rectangle we used in graphing the ellipse x^2 / a^2 + y^2 / b^2 = 1.
- We then sketch the diagonals of these rectangles.
- For the first equation, if y = 0 then x = +- a (note that x = 0 is impossible).
- We therefore start at the point
(a, 0), and sketch the right half of a hyperbola asymptotic to the diagonals, as shown in
blue.
- We then sketch the left half
starting at the point (-a, 0).
- For the second equation, if x = 0 then y = +- a (note that y = 0 is impossible).
- We start at the point (0, b) and
sketch the upper half of a parabola asymptotic to the diagonals, as shown in red.
- We then sketch the lower half
starting at the point (0, -b).
Video Clip #06