Precalculus II
Class Notes, 2/25/99
The figure below depicts a generally ellipse centered at the origin with semi-major
axis a in the x direction and semi-minor axis b in the y direction.
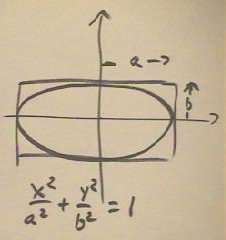
We can shift the position of the ellipse by x0 units in the horizontal and y0 units in
the vertical direction, obtaining the ellipse depicted in the figure below.
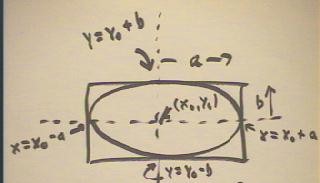
The equation of this ellipse is (x - x0) ^ 2 + (y - y0) ^ 2 = 1, as
indicated below.
- Replacing the x of x^2 / a^2 + y^2 / b^2 = 1 with (x - x0) and the y with (y - y0)
shifts the graph x0 units in the x direction and y0 units in the y direction.

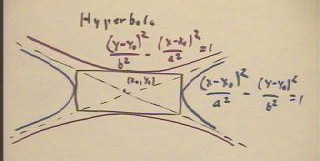
Similarly we shift a basic hyperbola by replacing x and y by (x - x0) and (y - y0), as
indicated below.
Video Clip #01
A parabola is the set of
points lying at equal distance from some straight line, called the directrix, and from
some point, called the focus.
- For the basic parabola depicted below, the focus is at (0, c) and the director
set y = -c.
- If (x, y) is any point in the plane, then its distance from the focus is d1 = `sqrt( (0
- x) ^ 2 + (c - y) ^ 2 ), and its distance from the directrix is d2 = | -c -y |.
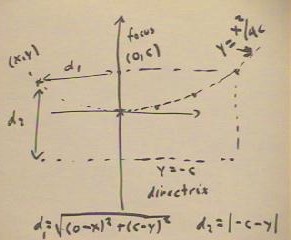
When the distances d1 and d2 are set equal we obtain the equation indicated below,
which is easily rearranged to obtain y = x^2 / ( 4 c ).
- This equation is easily recognized as the equation of the basic parabola y = x^2,
vertically stretched by factor 1 / ( 4 c ).
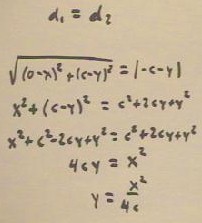
Video Clip #02
The point lying proportion t of the way from (x1, y1) to (x2, y2) is depicted in the
figure below.
- The point lies at x displacement t ( x2 - x1) and y displacement t (y2 - y1) from the
point (x1, y1).
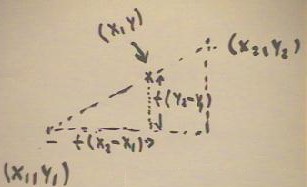
We thus see that, as depicted in figure below, x and y must satisfy the two equations
x = x1 + (x2 - x1) t,
y = y1 + (y2 - y1) t.
- The points for which t = 0, t = 1/2 and t = 1 are indicated in the figure below.
- These points lot along the straight line defined by the two points (x1, y1) and (x2,
y2).
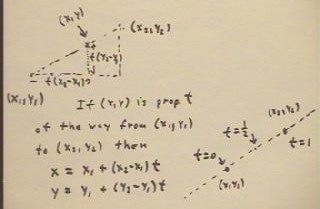
Video Clip #03
We call the two equations x = x1 + (x2 - x1) t, y = y1 + (y2 - y1) t the parametric
equations for the line.
- The variable t is the parameter, which is a variable quantity.
- As the parameter t varies over all possible real numbers, the corresponding points will
trace out the entire line defined by the two points.
- If t lies between 0 and 1, the corresponding point will lie between (x1, y1) and (x2,
y2).
- If t > 1, the corresponding point lies beyond (x2, y2).
- If t < 1, the corresponding point lies on the other side of (x1, y1) ('before' the
point).
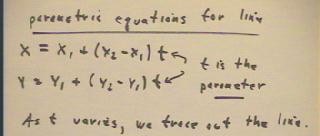
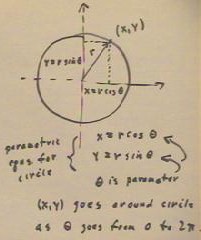
The circular definition of the sine and cosine functions provide another example of how
parametric equations can defined figures in the x-y plane.
- The parametric equations are x = r cos(`theta) and y = r sin (`theta).
- In this case the angle 'theta is the parameter; as `theta varies from 0 to 2 `pi the
corresponding points trace out a circle.
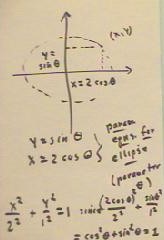
If we use different coefficients for the sine and cosine functions, we no longer get a
circle but and ellipse.
- In the example below we let x = 2 cos(`theta) and y = sin(`theta).
- Since (2 cos `theta ) ^2 / 2^2 + (sin `theta)^2 / 1^2 = cos^2(`theta) + sin^2(`theta) =
1, we see that x^2 / 2^2 + y^2 / 1^2 = 1, and as expected we have an ellipse with
semimajor axis 2 in the x direction and minor axis 1 in the y direction.
Video Clip #04
In response to a question posed in class, we complete the square to determine the graph
of the equation indicated in the figure below.
- In the third line we factor out the coefficients of x^2 and y^2.
- In the fourth and fifth lines we complete the squares on the x and the y quantities in
parentheses.
- In the six line we distribute the factor quantities back through the resulting
expressions.
- In the six line we move all constant terms to the right-hand side.
- In the last line we divide both sides by 48 in order to obtain 1 on the right-hand side.
- note error: the 48 should be 56: -16-9=-25 and adding 25 to both sides
gives us 31+25=56 on the right-hand side
- the values of a and b should therefore be a = `sqrt(14) and b = `sqrt(56/9)
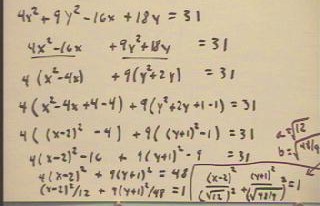
We finally put the equation into the standard form of an ellipse, showing that the
ellipse is centered at (2, -1) and has major axis `sqrt(12) in the next direction and
minor axis `sqrt(16/3) in the y direction.
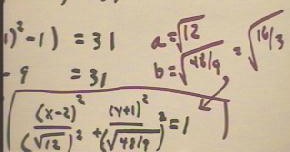
Video Clip #05
We plot the resulting ellipse below.
- The ellipse is centered at (2, -1) with the indicated major and minor axes.
- note that the previous error is continued here. a should be `sqrt(14) and b
should be `sqrt (56/9).
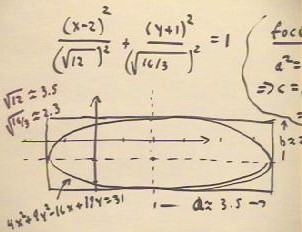
The foci of the ellipse lie at distances c = `sqrt(a^2 - b^2) to the right and left of
the center of the ellipse.
- You should calculate the value of c and determine the locations of the foci (one focus
is near the point (4.6, -1) ).
- the above coordinates of the focus are consistent with the erroneous values of a and
b shown in the figures; you should figure out also the coordinates of the focus of the
correct ellipse

Video Clip #06
