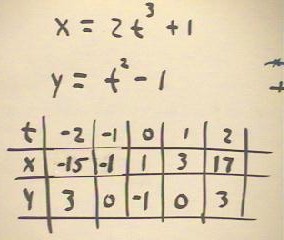
Precalculus II
Class Notes, 3/02/99
We first plot the parametric equations x = 2 t^3 + 1, y = t^2 - 1 by making a table, as indicated below.
We plot the corresponding points on the graph below, indicating the t values corresponding to each point.
The DERIVE expression [ 2 t^3 + 1, t^2 - 1 ] stands for the two parametric equations. When plotted, this expression gives a graph like that shown below.
We can express the equation of this curve in terms of just x and y by eliminating the parameter t.
We can eliminate the parameter `theta from the equations in the figure below.
We know in advance from previous work that these equations defined an ellipse with semi-axes 6 in the x direction and 2 in the y direction.
We could make a table and plot points; if you have not done so in a similar exercise, it is recommended that you do so now (use `theta values 0, `pi/6, `pi/3 and `pi/2 to start with; from the resulting points the rest of the points are fairly obvious).
To eliminate `theta, we begin by solving the first equation for `theta.
We obtain `theta = cos^-1 ( x / 6 ), which we substitute into the second equation.
To evaluate the resulting sin ( cos^-1( x/6) ), we proceed as in the following figure (you may consult this figure and return, or you may accept the result quoted here and then see where it came from after following the rest of this solution).
Our result is that sin (cos^-1(x / 6) ) = `sqrt( 6^2 - x^2 ) / 6.
We square both sides of the resulting equation, then simplify as indicated.
The expression cos^-1 ( x / 6 ) represents the angle whose cosine is x / 6.
Placing the x and y terms on the left-hand the constant terms on the right-hand side, we obtain the second line.
We see that the ellipse does indeed have semi-axes 6 and 2 in the x and y directions respectively.
In response to another question about completing the square, we determine the standard form of the equation indicated below.
In the figure below we first divide by the right-hand side to obtain 1 on that side.
In the second line we express the entire coefficient of each square as a denominator with a square.
We thus obtain a = `sqrt ( 33 / 4) and b = `sqrt(33); a simplifies to `sqrt(33) / 2, revealing that the x semi-axis is half that of the y semi-axis.