Class 00826

Day 1 Quiz 

1.  If you travel 300 miles in 6 hours what is your average speed?

 2.  How do you figure out average speed from how far and how long it took?  Don't quote some formula you remember from high school.  You almost certainly didn't use a formula to answer the first question and if you did you almost certainly didn't really need the formula.  What is the common sense of this situation?

 3.  If you travel at 60 miles an hour for 4 hours how far do you go?

 4.        You generalized question 1 when you answered question 2.  How can you generalize question 3?

First Experience with Pendulum

If a pendulum gets longer does it take more or less time to swing through one complete cycle back and forth?

 If one pendulum is twice as long as another will it take more than twice as long, less than twice as long or twice as long for it to swing through one complete cycle?

 If a sandbag is hanging from a 20-foot rope do you have to push harder to move it 2 feet from its 'natural, at-rest' position or to push it 4 feet from this position? 

Would the ratio of forces in the preceding question be 2-to-1, more than 2-to-1 or less that 2-to-1?

 Pendulum calibration

 Give a table showing the number of cycles in 30 seconds vs. the length in cm. of the pendulum.

 Give a table showing the number of second required for a single cycle of the pendulum vs. the length in cm. of the pendulum.

 When the calibration is complete write down the equation we obtained for the period of the pendulum as a function of it length in cm.

Here are data taken by the class:

length period cycles counted in 60 sec
20 0.909091 66
10 0.631579 95
6 0.550459 109
10 0.689655 87
20 0.909091 66
16 0.789474 76
19 0.857143 70
25 1 60
20 0.869565 69
7 0.566038 106
10 0.594059 101
22 0.9375 64
30 1.090909 55
20 0.895522 67
22 0.923077 65
5 0.46875 128
25 1 60
20 0.923077 65
20 0.909091 66
20 0.909091 66
30 0.75 80

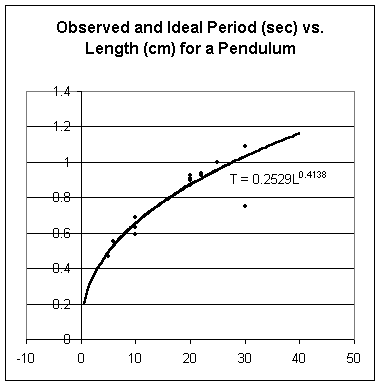
 A graph of observed period vs. length gives us the following graph and best-fit power function:

As we will see later in the course the theoretical function is T = .200 * L^.5 (approx).  This function is graphed on the same graph as the observed data.  We see that except for one clearly anomalous data point the 'ideal' function does a very good job of fitting the observed data.  The one anomalous point 'pulls down' the best-fit power function, resulting in the somewhat erroneous model T = .25 L^.41.

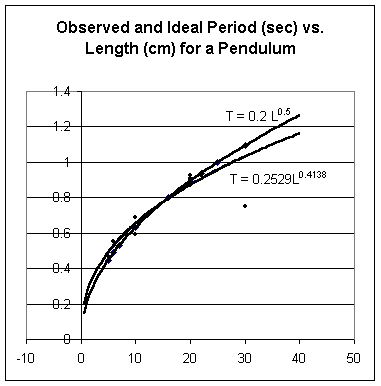
For reasons we will see later in the course the ideal function is y = .2 * L^.5

Marble exercise 

You have a marble and a ruler.  You can see the clock.  You can swing a pendulum, which you can also measure.  

Put the marble in a situation designed so that it travels a certain distance (you select the distance) in the same time interval every time the situation is repeated.  Make three trials and determine how fast the marble is moving in each trial.  Record the data you use to make your determination.

Was the marble's speed changing or constant during a given trial?  What makes you think so?

Did you measure an actual speed or the average of a changing speed?

If speed is changing then how do you measure the initial speed and the final speed over a given path?

Make the marble do something so it travels the same distance in the same time interval, three different times.  Use your pendulum to get the data you will need to determine how long it takes, and use your ruler to get data to figure out how far.

Homework:

Write two paragraphs to answer the following: