
Physics I Quiz 0906
If
you know v0, vf and `dt for a situation involving uniform acceleration which of
the following can you determine and how:
· vAve, `dv, `ds, a?
Construct a 'flow diagram' for the situation in which you are given v0, `dt and a.
If an object accelerates uniformly from rest through a displacement of 1.00 meter in .50 seconds then what is its acceleration?
Suppose that after a breakfast of Cheerios you go out to walk a quick mile with a very long, light and stretchy bungee cord attached to your belt. What you start out you feel very little resistance but as you walk you feel more and more resistance. Do you think you burn more Cheerios in the first or the second half of your walk? If the force exerted by the cord increases linearly with distance, how many times as much work do you think you do on the second half compared to the first half?
If you keep walking at the same pace what will happen to your heart rate? Why does this happen?
SOLUTIONS TO QUIZ:
If
you know v0, vf and `dt for a situation involving uniform acceleration which of
the following can you determine and how:
· vAve, `dv, `ds, a?
You can find all of these quantities. From vf and v0 you can find vAve = (vf + v0) / 2, since accel is uniform. From vf and v0 you can also find `dv = vf - v0. From vAve and `dt you can find `ds = vAve * `dt. From `dv and `dt you can find a = `dv / `dt.
The flow diagram below demonstrates the 'flow' of reasoning in this problem:

Construct a 'flow diagram' for the situation in which you are given v0, `dt and a.
From `dt and a we find `dv = a `dt. From v0 and `dv we find vf = v0 + `dv. From v0 and vf we find vAve = (vf + v0) / 2. From vAve and `dt we find `ds = vAve * `dt. The flow diagram below outlines this process:

You should understand all these relationships in terms of what happens when you drive your car (note, however, that the acceleration of your car is not uniform when you are starting out; constant pressure on your brakes tends to give you a constant negative acceleration). The figure below gives a specific example of the process outlined above.

If an object accelerates uniformly from rest through a displacement of 1.00 meter in .50 seconds then what is its acceleration?
The average velocity of the object will be vAve = `ds / `dt = 1.00 m / (.50 sec) = 2 m/s.
Since the object started from rest its final velocity must be 4 m/s. It change in velocity is therefore from 0 m/s to 4 m/s, a change of 4 m/s. So the acceleration is a = `dv / `dt = 4 m/s / (.5 s) = 8 m/s^2.
Suppose that after a breakfast of Cheerios you go out to walk a quick mile with a very long, light and stretchy bungee cord attached to your belt. What you start out you feel very little resistance but as you walk you feel more and more resistance. Do you think you burn more Cheerios in the first or the second half of your walk? If the force exerted by the cord increases linearly with distance, how many times as much work do you think you do on the second half compared to the first half?
If you pulled two bungee cords through the same distance you would experience double the force for that distance and you would store twice as much energy (the same as before in each of the two bungee cords), which would require you to do twice as much work against the resistance .
If you pull the bungee cord back twice as far then, if the force increases linearly with distance (not really so for most bungee cords but we assume it here) you will exert twice the force, on the average through twice the distance, resulting in four times as much work.
You do the same amount of work as before in the first half, so if you end up doing a total of four times as much, you do three times as much in the second half.
If you keep walking at the same pace what will happen to your heart rate? Why does this happen?
Every second the force increases as you move the same distance as in the last second. So you do more work each second, which means you have to burn more Cheerios each second, which requires more oxygen, which has to be pumped through your circulatory system. Your blood only holds so much oxygen so you've gotta circulate it faster. Your heart pumps pretty much the same amount of blood, and therefore oxygen, with each heartbeat. So heartrate increases.
From the First and Second Equations of Uniformly Accelerated Motion we can easily derive the Third and Fourth Equations of Uniformly Accelerated Motion:
The First and Second Equations are
`ds = (vf + v0) / 2 * `dt
vf = v0 + a `dt.
We solve by eliminating vf from the two equations to obtain the Third Equation, then we eliminate `dt to obtain the Fourth Equation.
The details by which we obtain the third equation `ds = v0 `dt + .5 a `dt^2:
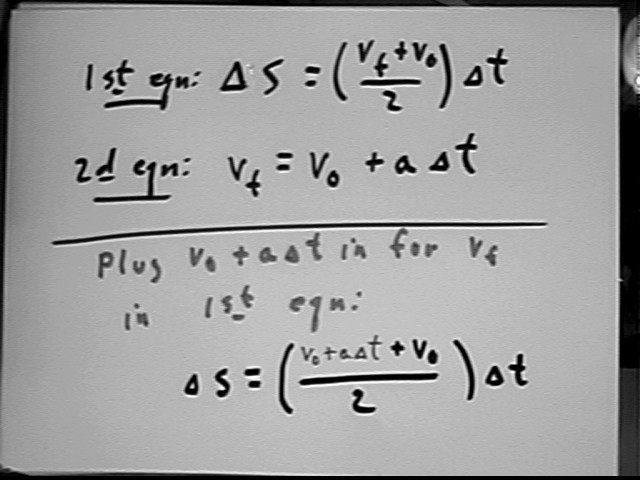
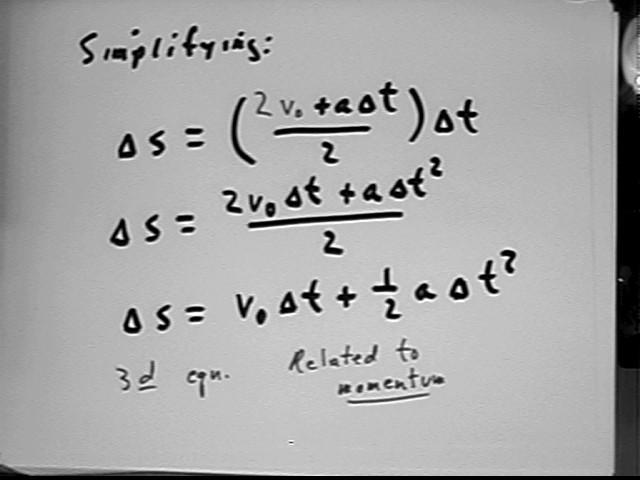
Note for future reference that the third equation is related to the concept of momentum.
To obtain the fourth equation we solve the second equation for `dt and substitute the resulting expression for `dt in the first:
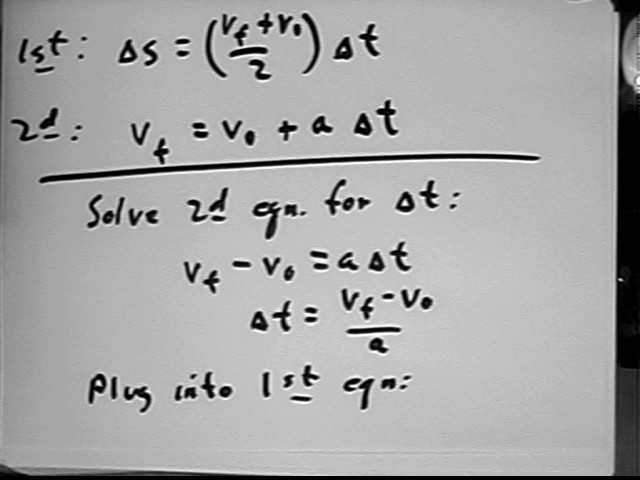
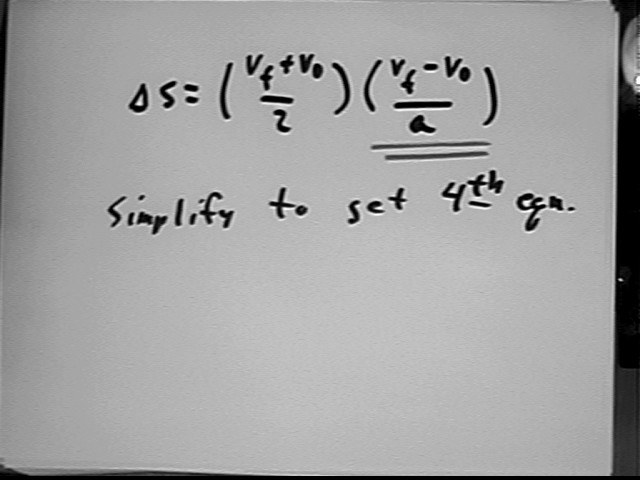
The class was asked to complete this derivation for homework.
We can represent a uniform acceleration situation by a trapezoid on a graph of v vs. t. For example in a situation where we're given v0, vf and `dt:

We see that the slope of the straight-line graph represents rise / run = change in v / change in t = rate of change of v or acceleration. The area of the trapezoid is ave ht * width, representing ave velocity * time interval or vAve * `dt = `ds.
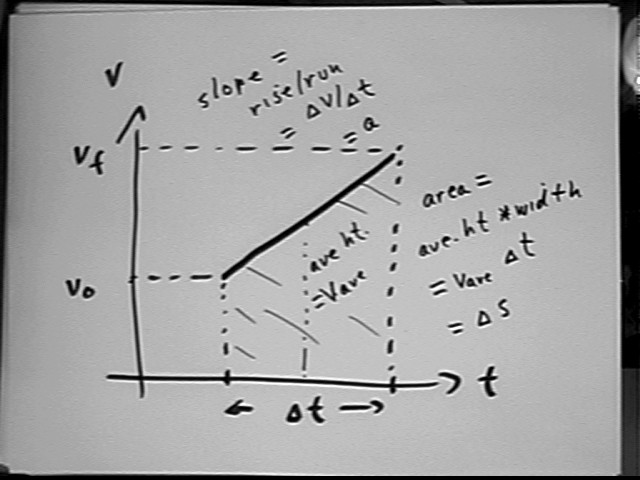
It is very important to understand that the slope of a v vs. t graph represents acceleration and that the area under a curve between two t values represents the displacement during that time interval. These statements are so even if the acceleration is not uniform.