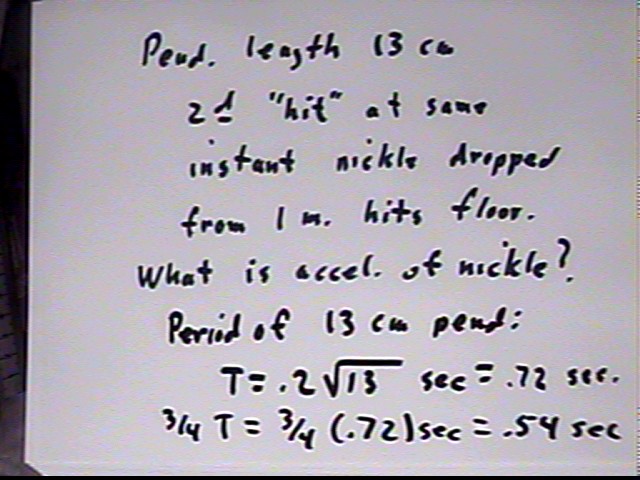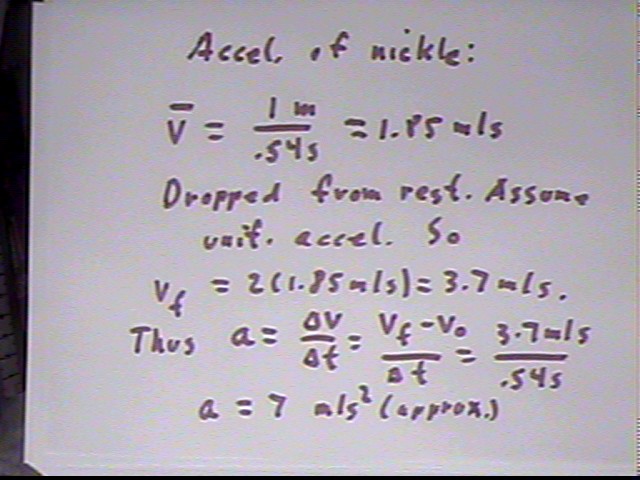Physics 1 Quiz 0909
Sketch the trapezoid corresponding to a uniform acceleration from velocity v0 to velocity vf in time interval `dt, where v0 and vf are the numbers of letters in your first and last name (if these are the same add the number of letters in your middle name to vf) and are regarded as being velocities in meters / second, and `dt is the number of letters in your middle name, regarded as being a time interval in seconds.
Use this trapezoid to determine the acceleration and displacement.
Sketch the flow diagram you would use to find acceleration and displacement.
How would you use the first two equations of motion to find acceleration and displacement?

The following were taken from work done on the 9/4 quiz.
Why
donít these make sense? Give
clear intuitive counterexamples. Describe
an experiment to test each hypothesis:
∑
vf = 2 * vAve:
disprove by driving for 1 hr at 60 mph without changing speed.
vf = vAve = 60 mph. Itís
not true that vf = 2 * vAve.
∑
`ds = vf / `dt:
disprove by driving for 1 hr at 60 mph without changing speed.
vf = vAve = 60 mph. But vf /
`dt= 60 mph / (1 hour) or 60 miles/hour^2, which isnít even a distance.
∑
a = vAve / `dt:
disprove by driving for 1 hr at 60 mph without changing speed.
vf = vAve = 60 mph. Velocity
hasnít changed so a = 0. vAve / `dt
isnít zero, a is zero.
∑
vAve = (vf Ė v0) / `dt:
This formula gives us units of (m/s) / s on the right-hand side and
m/s on the left. It CAINíT be
true. OR disprove by driving for 1
hr at 60 mph without changing speed. vf = v0 so vf-v0 = 0. But
average velocity isnít zero. So
the formula doesnít work.
Note
that the uniform-velocity situation is a good ĎB.S.-detectorí.
It doesnít always work. See
if you can find a feasible situation that would test each of the following:
∑
vf / 2 = vAve
∑
v0 / vf = `dt
∑
`dt / vf = `ds
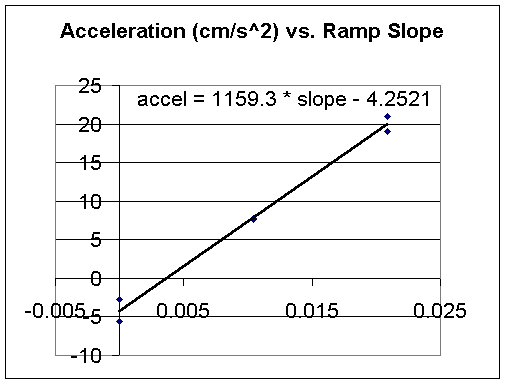
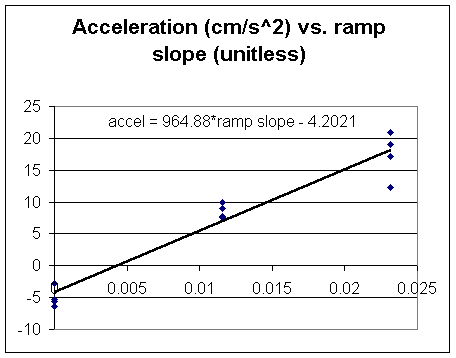
Acceleration vs. ramp slope data from last time were not submitted in a uniform format. The following graph was submitted from raw data submitted by two groups. Recall that timing was done using the pendulum timer, for a cart rolling 130 cm along a straight ramp at various inclines. Ramp slope was determined by the number of 5/8-inch boards under the legs of a table 5 feet in length. The graph is fit extremely well be a straight line. The slope of this straight line should ideally be equal to the acceleration of gravity, less about 1% to compensate for the friction in the cart's wheels:
Modifying for data from additional groups:
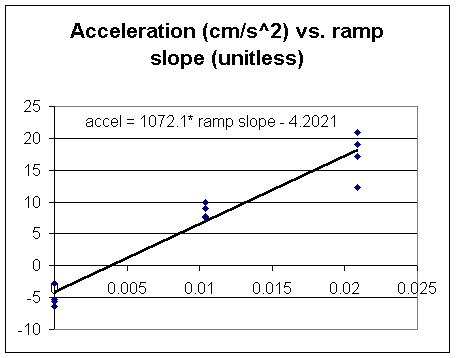
Slope calculation was initially based on a run of 5 feet (the length of the table) with, rise corresponding to the thickness of boards under the legs of the table. Run between the legs is only 54 inches. Correcting the slopes we obtain the following graph:
Results for the 4th equation of uniformly accelerated motion:
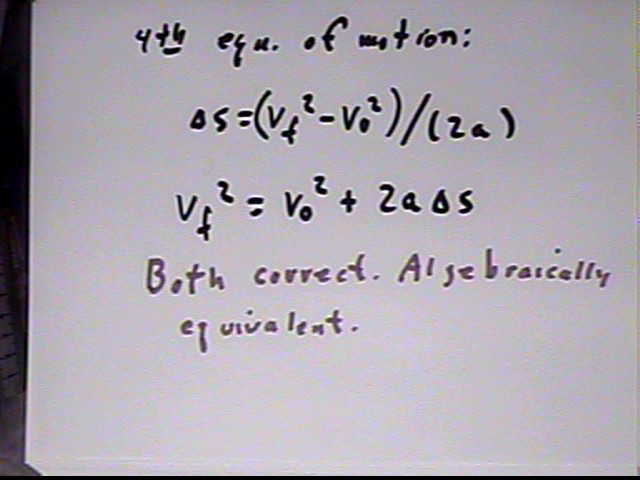
Reviewing how unif accel motion is analyzed and how the four equations of motion are obtained:
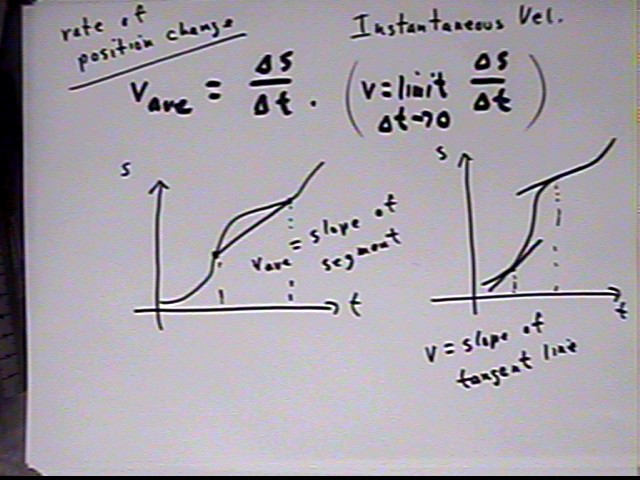
Velocity is the rate of change of position, which can be pictured as the slope of a graph of position s vs. clock time t:
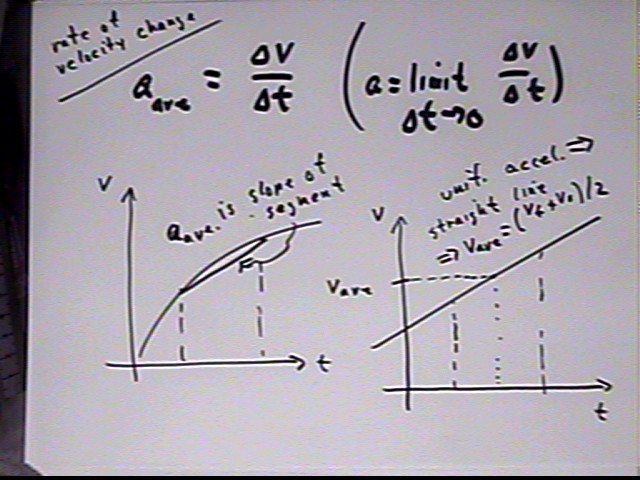
Acceleration is the rate of change of velocity, which can be pictured as the slope of a graph of velocity v vs. clock time t:
Uniformly accelerated motion can be understood in terms of the seven quantities `ds, `dt, vAve, vf, v0, `dv and a. All these quantities are required to understand what happens 'in front of your face' when an object accelerates uniformly.
Uniformly accelerated motion can modeled in terms of 5 equations, which unify our mathematical model of uniformly accelerated motion:

We note that if the 5 quantities v0, vf, `dt, a and `ds are known the quantities vAve and `dv are very easily found.
The algebraic steps from the definitions to the model are as follows:
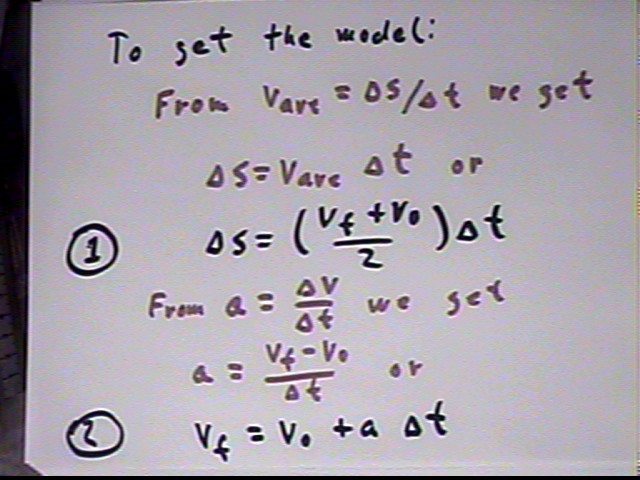

In a rough trial a pendulum of length 13 cm was observed to 'hit' for the second time at the same instant a nickel dropped simultaneously from a height of about 1 meter struck the floor. We find the acceleration of the nickel: