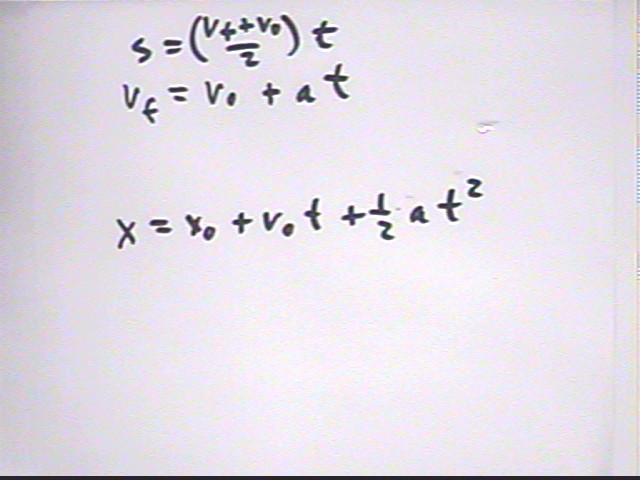Physics I Quiz 09/11/02
1. Briefly describe an experiment you would do to test each of the following, and explain how you expect the results would prove or disprove each:
`ds = (vf - v0) / 2 * `dt
·
v0 / vf = `dt
`dt / vf = `ds


2. Use the first two equations of uniformly accelerated motion to find the displacement and acceleration of an object whose initial velocity in m/s is equal to the number of letters in your middle name, whose final velocity over a time interval equal in seconds to the number of letters in your full name exceeds the initial (in m/s) by the number of letters in your first name.
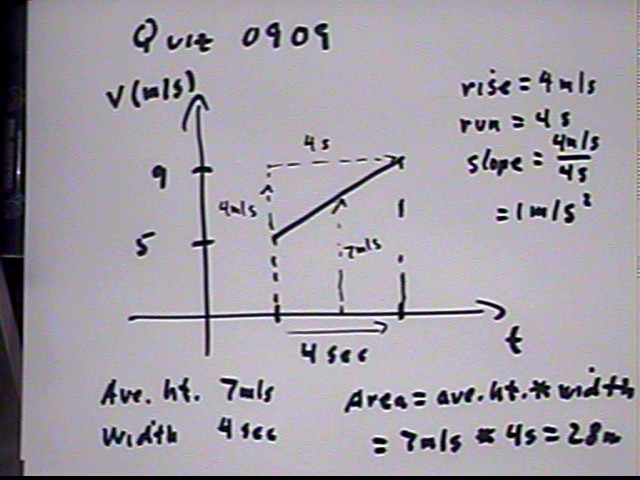


3. Use the fourth equation of uniformly accelerated motion to find the velocity attained by a ball whose initial velocity is 5 m/s and which accelerates uniformly at 2 m/s^2 as it travels 50 meters.

The following data and acceleration results were obtained by synchronizing the time of fall of a dropped object with the second 'hit' of a pendulum timer.
Note how the first set of data for a 10 cm pendulum showed a 'spread' in the drop heights corresponding to the characteristics of the different observers. These results are corroborated when independent observers repeat the experiment for the given pendulum lengths and drop heights. Note that the results obtained by this group averaged close to the ideal.
The group with the 12 cm pendulum had one result that was extremely inconsistent with the others.
Other groups had values that were 15% - 30% lower than the 'ideal' value. This might be explained if, for example, the determination of simultaneity was not independent among group participants but was instead a 'herd phenomenon' where perhaps everyone was influenced by the judgement of one individual who tended to anticipate the sounds.
| pend length | drop | accel |
|
14 |
27 |
171.4286 |
|
18 |
122 |
602.4691 |
|
10 |
110 |
977.7778 |
|
10 |
101 |
897.7778 |
|
10 |
105 |
933.3333 |
|
10 |
120 |
1066.667 |
|
10 |
112 |
995.5556 |
|
10 |
107 |
951.1111 |
|
12 |
85 |
629.6296 |
|
12 |
48 |
355.5556 |
|
12 |
81 |
600 |
|
10 |
90 |
800 |
|
10 |
96 |
853.3333 |
|
12 |
43 |
318.5185 |
|
10 |
98 |
871.1111 |
|
22 |
178 |
719.1919 |
|
22 |
166 |
670.7071 |
|
22 |
170 |
686.8687 |
|
22 |
177 |
715.1515 |
|
10 |
107 |
951.1111 |
|
16 |
116 |
644.4444 |
|
16 |
115 |
638.8889 |
|
16 |
122 |
677.7778 |
|
16 |
130 |
722.2222 |
|
16 |
122 |
677.7778 |
These results indicate some of the types of errors that can easily occur in even a simple experiment.
This experiment also indicates that it is indeed feasible to time events with reasonable accuracy using a synchronized pendulum when due to the short time period those events could not be accurately timed using, say, a stopwatch.
Your book's notation:
Your textbook, and traditional notation for the equations of motion, don't do a good job of distinguishing clock time from time interval, or change in position from position. Instead of `ds and `dt they will use s or x for the displacement of an object, and t for the time interval (this is not really so if you carefully read their conditions on the equations, but the traditional notation does tend to confuse time with time interval, etc.).
The notation used in this course emphasizes the interval nature of rate calculations. However, this notation has its own disadvantages. For example it becomes a bit confusing when we try to apply calculus to equations involving quantities like `ds and `dt.
The first two equations of motion will be presented in the General College Physics text as indicated below, using s and t instead of `ds and `dt. The first equation, for example, will be presented in the University Physics text using x for position, x0 for initial position and t instead of `dt. Be sure you understand the differences between your textbook's notation and the notation used in this course.