Notes from Class 0913

Physics I Quiz 0913

1.   For Physics 231, 241 (who should do it first; the problem is optional for everyone else, who should in any case save it for last):  In determining the acceleration of gravity by synchronizing a pendulum with a dropped object what percent error in the acceleration would result from an error of 3 millimeters in measuring a 10-cm pendulum?  How does the percent error in measurement compare with the percent error in the final result?

2.  Phy 121 and 201 only:  Suppose that observation indicates an object falls 4 meters in .9 seconds.  Assuming uniform acceleration, what is its acceleration?

3.  Assuming that the acceleration of gravity is 980 cm/s^2, if a dropped object falls from rest to the floor, falling through a number of centimeters equal to ten times the number of letters in your full name, how long will it take to fall?  How long would a pendulum timer have to be in order to synchronize the second 'hit' with the instant the object hits the floor? 

Answer the same questions for a 2-cm error in measuring a 100-cm fall.

SOLUTION:  Using `ds = 50 cm we see that we are given `ds, v0 and a.  The equation appropriate to this situation is the third equation `ds = v0 `dt + .5 a `dt^2, which since v0 = 0 we can easily solve for `dt.

Recalling that when L is in cm then period T in seconds is T = .2 sqrt(L), and using the fact that the time interval from release to second 'hit' corresponds to 3/4 of a cycle, we see that L corresponding to `dt = .32 sec is 

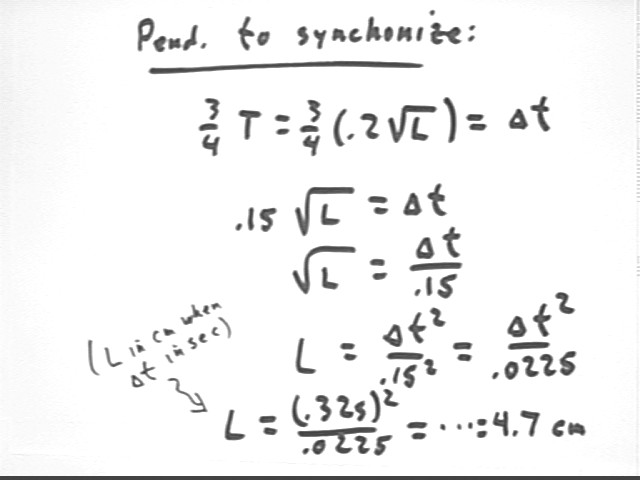
Quiz BS Detection

The following each appeared on more than one quiz today.  Test each against a simple situation to see if it holds.  Write up for next time.

What sort of experiment could we do with a marble, a straight ramp and a pendulum timer to test whether the acceleration on the ramp is independent of the speed of the marble and the position on the ramp?

Suggestions:  Determine acceleration in the following scenarios:

Every Group:  Get me a data report by 12:00 then take a 10-minute break.

All groups reported pendulum length, distance from rest down ramp and number of pendulum cycles:

First group's data:

13 40 3.75
13 60 4.5
13 80 5
13 100 6
13 120 7

Note that the first group tried to estimate fractions of a pendulum half-cycle rather than synchronizing the pendulum, which tends to result in less accuracy.

Acceleration vs. distance graph

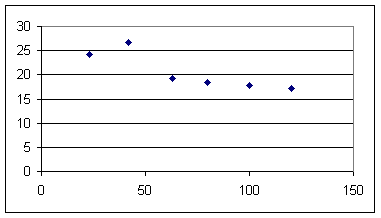
Second group's data:

13 60 4.5
13 80 5
13 100 6

This group also attempted to estimate fractions of half-cycles.  Also the range of ramp lengths was limited.  

Third group:

10 20 3
10 40 4
10 60 5
10 80 6
10 100 6

It appears unlikely that the ball rolled the last 20 cm instantaneously, so the last two timings indicate that the pendulum probably was not carefully enough synchronized.

Fourth group:

15.5 23 4
15.5 42 5
15.5 63 7
15.5 80 8
15.5 100 9
15.5 120 10

This data would indicate that the object slowed considerably between the 42 cm position and the 63 cm position, which is unlikely.  It appears that synchronization was imperfect.

Homework:  Complete your own analysis of your groups data.

Decide whether the data obtained by the different groups supports or does not support the hypothesis that acceleration is the same everywhere on the ramp independent of the speed of the object, within the limits of accuracy of the apparatus.

If the hypothesis does not seem to be supported analyze whether human error or the limitations of equipment were responsible. 

Text Homework: