Notes from Class 0916

Physics I Quiz 0916

1.  A pendulum timer which is determined to have a length of 16 cm is synchronized so that on its seventh 'hit' an object which is released from rest at the same instant as the pendulum will be at position 140 cm down a ramp.

If the measurement was in fact 3 mm less than the actual length of the pendulum what acceleration is indicated?

If the measurement was in fact 3 mm more  than the actual length of the pendulum what acceleration is indicated?

What therefore would we say is the uncertainty in acceleration if the uncertainty in the length of this pendulum is 3 mm?

What is this uncertainty as a percent of the acceleration?

SOLUTION:

We first calculate the period of the pendulum at the 16 cm length, and also at lengths 15.7 cm (3 mm shorter) and 16.3 cm ( 3 mm longer).

Then we determine the time require for 7 'hits'.

From the 140 cm displacement and the 'high' and 'low' time intervals we find the corresponding respective low and high values of acceleration.

We calculate percent uncertainty by finding the difference from the approximate 'midway' acceleration to the extreme high or low acceleration as a proportion of the 'midway' acceleration.  We then convert to percent.

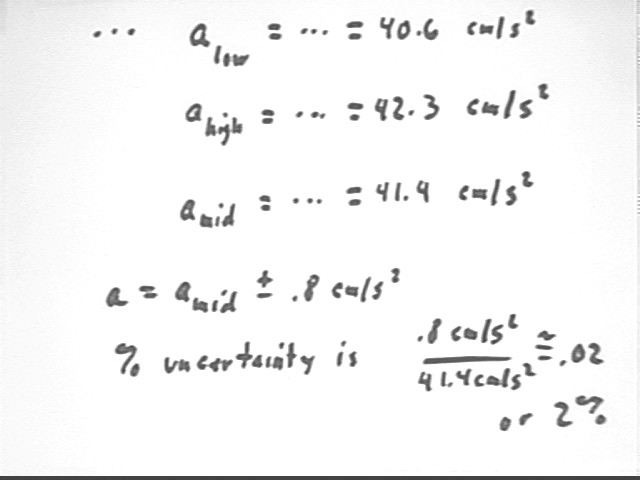
For comparison we calculate the percent uncertainty in length and in the period of the pendulum.  We note that a 2% uncertainty in length leads to a 1% uncertainty in time interval, which leads to a 2% uncertainty in acceleration.  

 

2.  If an object is thrown in the downward direction at 5 m/s, after which is accelerates at the acceleration of gravity, how long will it take to reach the ground 50 meters below?

SOLUTION:  If we choose downward as the positive direction we know that v0 = 5 m/s^2, `ds = 50 m and a = 9.8 m/s^2.  This situation is not amenable to direct reasoning so we use the Fourth Equation of Motion vf^2 = v0^2 + 2 a `ds to determine final velocity.  We then use average velocity and time displacement to find time interval.  We end up with `dt = 2.72 s.

By how many seconds will the object 'beat' an object to the ground if the object is dropped simultaneously from rest at the position at release position of the first object?

SOLUTION:  We can use the same procedure as before.  We get `dt = 3.19 s.

The first object will 'beat' the second by .47 seconds.

A weight supported by my hand, not moving, is in equilibrium--zero net force.  The downward force exerted by gravity is balanced by the upward force exerted by my hand.

If there is a nonzero net force (net force is the sum of all forces acting on the object) the object will accelerate in the direction of the net force.

Using 4 rubber bands in series, stretch them to a fixed length sufficient to accelerate an empty roller-chair.  Record the length, the distance accelerated from rest and the time required to accelerate through that distance.

Repeat for a significantly different length.

Repeat a third time for a length significantly different than those used previously.

Determine acceleration of freely pushed chair.

Find acceleration of chair vs. length of rubberband.

Graph accel of chair vs. length of rubberband.

Will the acceleration vs. rubberband length look more like the first, second or third curve in the figure below?  What else about this figure will be different for this experiment? 

 

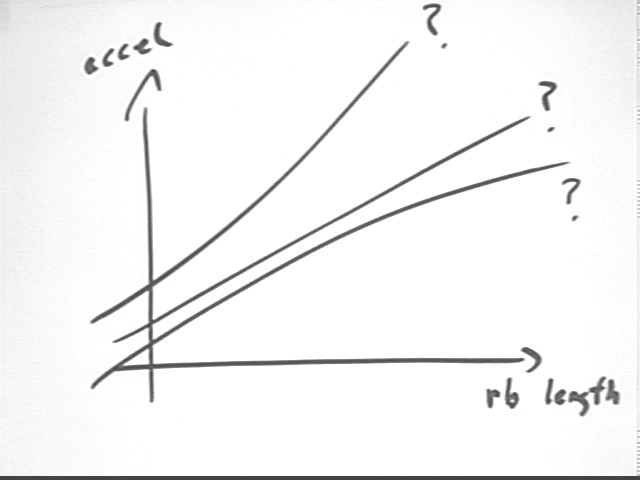
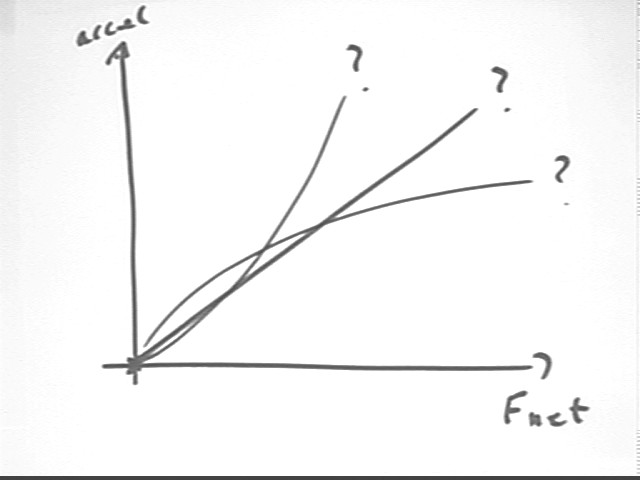
Rubberband tension is not a linear function of length.  If we were to graph acceleration vs. net force, which graph would we end up with?

We note that zero net force implies zero acceleration, any positive net force implies a positive acceleration, which is consistent with our experience during the experiment.

Results of the experiment (graphs of accel in cm/s^2 vs. rubberband length in cm, with assumption of 'slack' length of 8 cm):

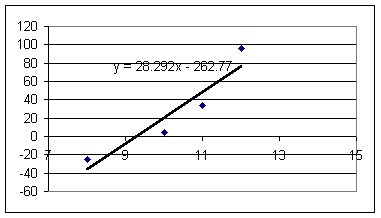
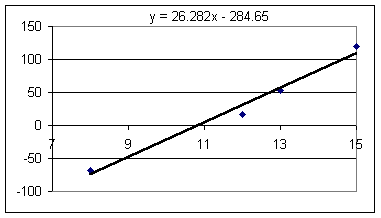
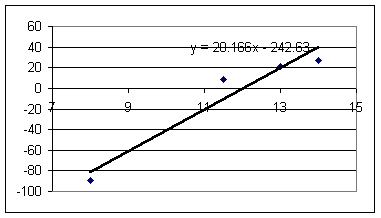
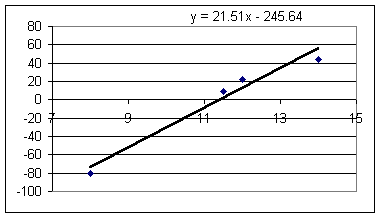
Estimating approximately .6 N of force per rubberband for every cm of rubberband length in excess of the 8 cm 'slack' length, and adding to each acceleration the magnitude of the 'coasting' acceleration to correct for frictional resistance we get the following graphs of accel in cm/s^2 vs. force in Newtons (note that these units aren't really compatible, as we'll see soon).

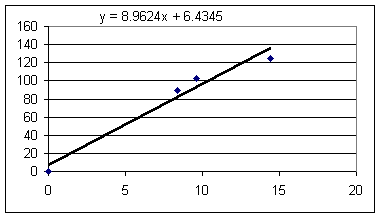
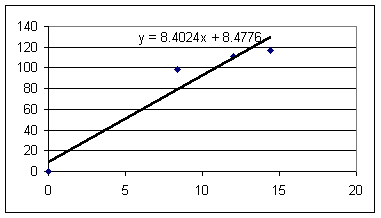
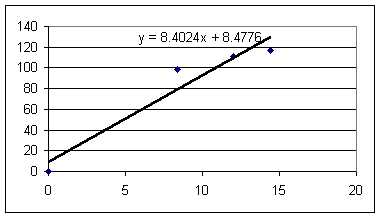
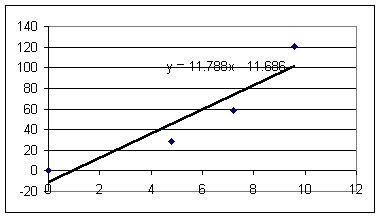
These results indicate slopes ranging from 8.4 to 11.8 cm/s^2 / Newton.  The vertical-axis intercepts are generally within 10 cm/s^2 of the axis and therefore aren't very significant in comparison with the uncertainties evident in the data, so it's not unreasonable to presume a linear proportionality between acceleration and net force.  

An approximate mean proportionality of acceleration to net force would be in the neighborhood of 

From these data we will be able to estimate the masses of the chairs.

Newton's Third Law:  An object at rest will remain at rest, and an object in motion will remain in motion with unchanging speed and direction, unless acted on by a nonzero net force.

Newton's Second Law:  The acceleration of an object is directly proportional to the net force acting on it.